悠日記: 上帝擲骰子嗎？測不準原理和隱變數理論

測不準原理，又稱海森堡測不準原理，是量子力學中的一個基本概念。它指出，同時知道某些物理屬性對（例如位置和動量）的精度是有限的。換句話說，一個屬性測量得越準確，另一個屬性的了解就越不準確。

更正式地說，不確定性原理是各種數學不等式中的任何一種，它對量子系統上某些相關測量對（例如位置x和動量p ）的精度的乘積提出了基本限制。^[ 1 ]這種配對變數稱為互補變數或規範共軛變數。

德國物理學家Werner Heisenberg於 1927 年首次提出，^[ 2 ]^[ 3 ]^[ 4 ]^[ 5 ]與位置σ _x的標準差和動量σ _p的標準差相關的形式不等式由Earle Hesse Kennard導出^[⁶^]同年稍後以及Hermann Weyl ^[⁷^]在 1928 年提出：

$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}$

在哪裡 $\hbar ={\frac {h}{2\pi }}$ 是簡化的普朗克常數。

典型的量子力學不確定性原理除了位置動量之外還有多種形式。能量-時間關係被廣泛用於將量子態壽命與測量的能量寬度聯繫起來，但其形式推導充滿了關於時間本質的令人困惑的問題。基本原理已向多個方向擴展；在許多種基本物理測量中都必須考慮它。

位置-動量

多個平面波疊加形成波包。隨著許多波的添加，該波包變得越來越局域化。傅立葉變換是一種數學運算，可將波包分離成單獨的平面波。此處顯示的波浪是真實的，僅用於說明目的；在量子力學中，波函數通常是複雜的。

說明該原理如何應用於相對可理解的物理情況至關重要，因為它在人類經驗的宏觀^[ 8 ]尺度上是難以辨別的。量子物理學的兩種替代框架對不確定性原理提供了不同的解釋。不確定性原理的波動力學圖在視覺上更加直觀，但更抽象的矩陣力學圖以更容易推廣的方式來表達它。

從數學上講，在波力學中，位置和動量之間存在不確定性關係，是因為波函數在希爾伯特空間中對應的兩個正交基底中的表達式是彼此的傅立葉變換（即位置和動量是共軛變數）。非零函數及其傅立葉變換不能同時被銳定域。^[⁹^]傅立葉共軛變異數之間的類似權衡出現在傅立葉分析所依據的所有系統中，例如在聲波中：純音是單一頻率處的尖銳尖峰，而其傅立葉變換給出了聲波的形狀在時域中，這是一個完全離域的正弦波。在量子力學中，兩個關鍵點是粒子的位置採用物質波的形式，動量是其傅立葉共軛，由德布羅意關係 $p$ $=$ $ħk$ 保證，其中 $k$ 是波數。

在矩陣力學（量子力學的數學公式）中，任何一對代表可觀測量的非對易自共算子都受到類似的不確定性限制。可觀測量的本徵態表示特定測量值（本徵值）的波函數狀態。例如，如果執行可觀測量 $A$ 的測量，則系統處於該可觀測量的特定本徵態 $Ψ$ 。然而，可觀測量 $A$ 的特定本徵態不必是另一個可觀測量 $B$ 的本徵態：如果是這樣，則它沒有唯一的關聯測量，因為系統不處於該可觀測量的本徵態。^[¹⁰^]

視覺化

對於具有一維質量的無自旋粒子，可以使用位置空間波函數和動量空間波函數來視覺化不確定性原理。

位置空間波函數越局域化，越有可能在該區域中找到具有位置座標的粒子，相應地，動量空間波函數局域化程度越低，因此粒子可能具有的動量分量越廣泛。相反，動量空間波函數越局域化，粒子越有可能在該區域中找到具有動量分量值的粒子，相應地，位置空間波函數局域化越少，因此粒子可以佔據的位置坐標為更廣泛。這些波函數是彼此的傅立葉變換：在數學上，不確定性原理表達了變換中共軛變數之間的關係。

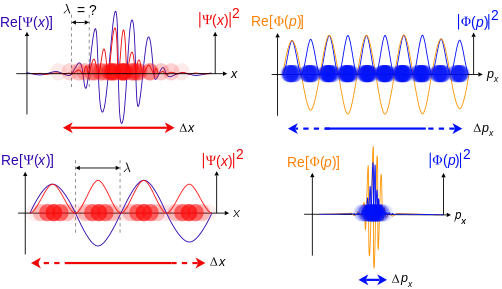
波力學解釋

平面波

波包

德布羅意波在一維中的傳播－複振幅的實部為藍色，虛部為綠色。在給定點x找到粒子的機率（顯示為顏色不透明度）像波形一樣展開，粒子沒有確定的位置。當振幅增加到零以上時，曲率符號反轉，因此振幅開始再次減小，反之亦然 - 結果是交替振幅：波。

根據德布羅意假說，宇宙中的每個物體都與波有關。因此，每一個物體，從基本粒子到原子、分子，一直到行星甚至更遠的地方，都受到測不準原理的約束。

波數k ₀或動量p ₀的單模平面波的與時間無關的波函數為^[ 11 ] $\psi (x)\propto e^{ik_{0}x}=e^{ip_{0}x/\hbar }~.$

玻恩規則指出，這應該被解釋為機率密度振幅函數，即找到a和b之間的粒子的機率為 $\operatorname {P} [a\leq X\leq b]=\int _{a}^{b}|\psi (x)|^{2}\,\mathrm {d} x~.$

對於單模平面波， $|\psi (x)|^{2}$ 是1如果 $X=x$ 否則為0。換句話說，粒子位置極為不確定，因為它基本上可能位於波包上的任何位置。

另一方面，考慮一個波函數，它是許多波的總和，我們可以將其寫為 $\psi (x)\propto \sum _{n}A_{n}e^{ip_{n}x/\hbar }~,$ 其中A _n表示眾數p _n對總體的相對貢獻。右圖顯示了透過添加許多平面波，波包如何變得更加局域化。我們可以更進一步達到連續極限，其中波函數是所有可能模式的積分。 $\psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }\varphi (p)\cdot e^{ ipx/\hbar }\,dp~,$ 和 $\varphi (p)$ 表示這些模式的振幅，稱為動量空間中的波函數。用數學術語來說，我們說 $\varphi (p)$ 是傅立葉變換 $\psi (x)$ x和p是共軛變數。將所有這些平面波加在一起是有代價的，即動量變得不那麼精確，變成了許多不同動量的波的混合物。^[ 12 ]

量化位置和動量精度的一種方法是標準差 σ。自從 $|\psi (x)|^{2}$ 是位置的機率密度函數，我們計算它的標準差。

透過使用較多的平面波，提高了位置精度，即減小了σ _x，從而削弱了動量的精度，即增大了σ _p。表述這一點的另一種方式是σ _x和σ _p具有反比關係或至少受下界限制。這就是不確定原理，精確極限是肯納德界。

用波力學證明肯納德不等式

我們感興趣的是位置和動量的方差，定義為 $\sigma _{x}^{2}=\int _{-\infty }^{\infty }x^{2}\cdot |\psi (x)|^{2}\,dx-\左(\int _{-\infty }^{\infty }x\cdot |\psi (x)|^{2}\,dx\right)^{2}$ $\sigma _{p}^{2}=\int _{-\infty }^{\infty }p^{2}\cdot |\varphi (p)|^{2}\,dp-\左(\int _{-\infty }^{\infty }p\cdot |\varphi (p)|^{2}\,dp\right)^{2}~.$

不失一般性，我們將假設平均值消失，這相當於座標原點的移動。（下面給出了不做出這種假設的更一般的證明。）這給了我們更簡單的形式 $\sigma _{x}^{2}=\int _{-\infty }^{\infty }x^{2}\cdot |\psi (x)|^{2}\,dx$ $\sigma _{p}^{2}=\int _{-\infty }^{\infty }p^{2}\cdot |\varphi (p)|^{2}\,dp~。$

功能 $f(x)=x\cdot \psi (x)$ 可以解釋為函數空間中的向量。我們可以為這個向量空間中的一對函數u ( x ) 和v ( x )定義內積： $\langle u\mid v\rangle =\int _{-\infty }^{\infty }u^{*}(x)\cdot v(x)\,dx,$ 其中星號表示複共軛。

定義了這個內積後，我們注意到位置的變異數可以寫成 $\sigma _{x}^{2}=\int _{-\infty }^{\infty }|f(x)|^{2}\,dx=\langle f\mid f\rangle ~ .$

我們可以透過解釋函數來重複這個動量 ${\tilde {g}}(p)=p\cdot \varphi (p)$ 作為向量，但我們也可以利用以下事實： $\psi (x)$ 和 $\varphi (p)$ 是彼此的傅立葉變換。我們透過分部積分來評估傅立葉逆變換： ${\begin{對齊}g(x)&={\frac {1}{\sqrt {2\pi \hbar }}}\cdot \int _{-\infty }^{\infty }{\波形符號{g}}(p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\ infty }^{\infty }p\cdot \varphi (p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{2\pi \hbar }}\int _{ - \infty }^{\infty }\left[p\cdot \int _{-\infty }^{\infty }\psi (\chi )e^{-ip\chi /\hbar }\,d\chi \右]\cdot e^{ipx/\hbar }\,dp\\&={\frac {i}{2\pi }}\int _{-\infty }^{\infty }\left[{\取消{\left.\psi (\chi )e^{-ip\chi /\hbar }\right|_{-\infty }^{\infty }}}-\int _{-\infty }^{\ infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\ , dp\\&=-i\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}\left[{\frac {1}{2 \ pi }}\int _{-\infty }^{\infty }\,e^{ip(x-\chi )/\hbar }\,dp\right]\,d\chi \\&=-i \ int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}\left[\delta \left({\frac {x-\chi }{\ hbar }}\right)\right]\,d\chi \\&=-i\hbar \int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\ chi }}\left[\delta \left(x-\chi \right)\right]\,d\chi \\&=-i\hbar {\frac {d\psi (x)}{dx}}\ \ &=\left(-i\hbar {\frac {d}{dx}}\right)\cdot \psi (x),\end{對齊}}$ 在哪裡 $v={\frac {\hbar }{-ip}}e^{-ip\chi /\hbar }$ 在分部積分中，被取消的項消失，因為波函數在無限遠處消失，最後兩次積分重新啟用傅立葉變換。常出現這個詞 ${\textstyle -i\hbar {\frac {d}{dx}}}$ 稱為位置空間中的動量算符。應用Plancherel 定理，然後應用Parseval 定理，我們看到動量的變異數可以寫成 $\sigma _{p}^{2}=\int _{-\infty }^{\infty }|{\tilde {g}}(p)|^{2}\,dp=\int _ {-\infty }^{\infty }|g(x)|^{2}\,dx=\langle g\mid g\rangle .$

柯西-施瓦茨不等式斷言 $\sigma _{x}^{2}\sigma _{p}^{2}=\langle f\mid f\rangle \cdot \langle g\mid g\rangle \geq |\langle f\mid g\rangle |^{2}~.$

任何複數z的模平方可以表示為 $|z|^{2}={\Big (}{\text{Re}}(z){\Big )}^{2}+{\Big (}{\text{Im}}(z ){\Big )}^{2}\geq {\Big (}{\text{Im}}(z){\Big )}^{2}=\left({\frac {zz^{\ast } {2i}}\右)^{2}.$ 我們讓 $z=\langle f|g\rangle$ 和 $z^{*}=\langle g\mid f\rangle$ 並將這些代入上面的等式中得到 $|\langle f\mid g\rangle |^{2}\geq \left({\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}\right )^{2}~.$

剩下的就是評估這些內積。

${\begin{對齊}\langle f\mid g\rangle -\langle g\mid f\rangle &=\int _{-\infty }^{\infty }\psi ^{*}(x) \,x\cdot \left(-i\hbar {\frac {d}{dx}}\right)\,\psi (x)\,dx-\int _{-\infty }^{\infty }\ psi ^{*}(x)\,\left(-i\hbar {\frac {d}{dx}}\right)\cdot x\,\psi (x)\,dx\\&=i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\left[\left(-x\cdot {\frac {d\psi (x)}{dx}}\右)+{\frac {d(x\psi (x))}{dx}}\right]\,dx\\&=i\hbar \cdot \int _{-\infty }^{\infty }\ psi ^{*}(x)\left[\left(-x\cdot {\frac {d\psi (x)}{dx}}\right)+\psi (x)+\left(x\cdot { \frac {d\psi (x)}{dx}}\right)\right]\,dx\\&=i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{* }(x)\psi (x)\,dx\\&=i\hbar \cdot \int _{-\infty }^{\infty }|\psi (x)|^{2}\,dx\\\ &=i\hbar \end{對齊}}$

將其代入上述不等式中，我們得到 $\sigma _{x}^{2}\sigma _{p}^{2}\geq |\langle f\mid g\rangle |^{2}\geq \left({\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}\right)^{2}=\left({\frac {i\hbar }{2i}}\right)^{2} ={\frac {\hbar ^{2}}{4}}$ 或取平方根 $\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}~.$

當且僅當p和x線性相關時，相等。請注意，該證明中涉及的唯一物理原理是 $\psi (x)$ 和 $\varphi (p)$ 是位置和動量的波函數，它們是彼此的傅立葉變換。對於任何一對共軛變量，類似的結果都成立。

矩陣力學解釋

在矩陣力學中，位置和動量等可觀測量由自伴算符表示。^[ 12 ]當考慮成對的可觀測量時，一個重要的量是換向器。對於一對運算子 $和$ ${\hat {B}}$ ，將其換向器定義為 $[{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}} .$ 在位置和動量的情況下，換向器是典型的換向關係 $[{\hat {x}},{\hat {p}}]=i\hbar .$

非交換性的物理意義可以透過考慮換向器對位置和動量本徵態的影響來理解。讓 $|\psi \rangle$ 是具有恆定特徵值 $x 0$ 的位置的右側徵態。根據定義，這意味著 ${\hat {x}}|\psi \rangle =x_{0}|\psi \rangle .$ 將換向器應用於 $|\psi \rangle$ 產量 $[{\hat {x}},{\hat {p}}]|\psi \rangle =({\hat {x}}{\hat {p}}-{\hat {p}}{ \hat {x}})|\psi \rangle =({\hat {x}}-x_{0}{\hat {I}}){\hat {p}}\,|\psi \rangle =i \hbar |\psi \rangle ,$ 其中 $Î$ 是恆等運算子。

假設，為了反證法， $|\psi \rangle$ 也是動量的右本徵態，具有恆定的特徵值 $p 0$ 。如果這是真的，那麼人們可以寫 $({\hat {x}}-x_{0}{\hat {I}}){\hat {p}}\,|\psi \rangle =({\hat {x}}-x_{ 0}{\hat {I}})p_{0}\,|\psi \rangle =(x_{0}{\hat {I}}-x_{0}{\hat {I}})p_{0 }\,|\psi \角=0.$ 另一方面，上述規範交換關係要求 $[{\hat {x}},{\hat {p}}]|\psi \rangle =i\hbar |\psi \rangle \neq 0.$ 這意味著沒有量子態可以同時是位置和動量本徵態。

當測量一個狀態時，它會根據相關可觀測量被投影到本徵態上。例如，如果測量了粒子的位置，則該狀態相當於位置本徵態。然而，這意味著該狀態不是動量本徵態，而是可以表示為多個動量基本徵態的總和。換句話說，動量必須不太精確。此精度可以透過標準差來量化， $\sigma _{x}={\sqrt {\langle {\hat {x}}^{2}\rangle -\langle {\hat {x}}\rangle ^{2}}}$ ${\displaystyle \sigma _{p}={\sqrt {\langle {\hat {p}}^{2}\rangle -\langle {\hat {p}}\rangle ^{2}}}。$

正如上面的波浪力學解釋一樣，人們可以看到兩者各自精度之間的權衡，並透過不確定性原理進行量化。

量子諧振子穩態

考慮一維量子諧振子。可以用創造和湮滅算符來表達位置和動量算符： ${\hat {x}}={\sqrt {\frac {\hbar }{2m\omega }}}(a+a^{\dagger })$ ${\hat {p}}=i{\sqrt {\frac {m\omega \hbar }{2}}}(a^{\dagger }-a).$

使用能量本徵態的創建和湮滅算符的標準規則， $a^{\dagger }|n\rangle ={\sqrt {n+1}}|n+1\rangle$ $a|n\rangle ={\sqrt {n}}|n-1\rangle ,$ 方差可以直接計算， $\sigma _{x}^{2}={\frac {\hbar }{m\omega }}\left(n+{\frac {1}{2}}\right)$ $\sigma _{p}^{2}=\hbar m\omega \left(n+{\frac {1}{2}}\right)\,.$ 這些標準差的乘積就是 $\sigma _{x}\sigma _{p}=\hbar \left(n+{\frac {1}{2}}\right)\geq {\frac {\hbar }{2}}.~$

特別地，上述肯納德界限^[ 6 ]對於基態 $n =0$ 是飽和的，此時機率密度恰好是常態分佈。

具有高斯初始條件的量子諧振子

初始高斯分佈的位置（藍色）和動量（紅色）機率密度。由上到下，動畫顯示Ω = ω、Ω = 2 ω和Ω = ω /2的情況。請注意分佈寬度之間的權衡。

在特徵角頻率ω的量子諧振子中，放置一個從位底偏移一定位移x ₀的狀態，如下圖所示 $\psi (x)=\left({\frac {m\Omega }{\pi \hbar }}\right)^{1/4}\exp {\left(-{\frac {m\Omega ) (x-x_{0})^{2}}{2\hbar }}\right)},$ 其中 Ω 描述初始狀態的寬度，但不必與ω 相同。透過對傳播器的積分，我們可以求解完全依賴時間的解決方案。經過多次取消後，機率密度降低為 $|\Psi (x,t)|^{2}\sim {\mathcal {N}}\left(x_{0}\cos {(\omega t)},{\frac {\hbar }{ 2m\Omega }}\left(\cos ^{2}(\omega t)+{\frac {\Omega ^{2}}{\omega ^{2}}}\sin ^{2}{(\omega t)}\右)\右)$ $|\Phi (p,t)|^{2}\sim {\mathcal {N}}\left(-mx_{0}\omega \sin(\omega t),{\frac {\hbar m \Omega }{2}}\left(\cos ^{2}{(\omega t)}+{\frac {\omega ^{2}}{\Omega ^{2}}}\sin ^{2} {(\omega t)}\右)\右),$ 我們使用符號的地方 ${\mathcal {N}}(\mu ,\sigma ^{2})$ 表示平均值μ和變異數σ ²的常態分佈。複製上面的變異數並應用三角恆等式，我們可以將標準差的乘積寫成 ${\begin{對齊}\sigma _{x}\sigma _{p}&={\frac {\hbar }{2}}{\sqrt {\left(\cos ^{2}{(\歐米茄t)}+{\frac {\歐米茄^{2}}{\歐米茄^{2}}}\sin ^{2}{(\歐米茄t)}\right)\left(\cos ^{2} {(\omega t)}+{\frac {\omega ^{2}}{\Omega ^{2}}}\sin ^{2}{(\omega t)}\right)}}\\&= {\frac {\hbar }{4}}{\sqrt {3+{\frac {1}{2}}\left({\frac {\Omega ^{2}}{\omega ^{2}}} +{\frac {\omega ^{2}}{\Omega ^{2}}}\right)-\left({\frac {1}{2}}\left({\frac {\Omega ^{2 }}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Omega ^{2}}}\right)-1\right)\cos {(4\omega t)} }}\end{對齊}}$

從關係來看 ${\frac {\Ω ^{2}}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Ω ^{2}}}\geq 2,\quad |\cos(4\omega t)|\leq 1,$ 我們可以得出以下結論（最右邊等式僅在Ω = ω時成立）： $\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{4}}{\sqrt {3+{\frac {1}{2}}\left({\frac {\歐米茄^{2}}{\歐米茄^{2}}}+{\frac {\歐米茄^{2}}{\歐米茄^{2}}}\right)-\left({\frac {1 }{2}}\left({\frac {\歐米茄^{2}}{\歐米茄^{2}}}+{\frac {\歐米茄^{2}}{\歐米茄^{2}}}\右)-1\右)}}={\frac {\hbar }{2}}.$

相干態

相干態是湮沒算子的右本徵態， ${\hat {a}}|\alpha \rangle =\alpha |\alpha \rangle ,$ 可以用福克狀態表示為 $|\alpha \rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over { \sqrt {n!}}}|n\rangle$

在相干態是量子諧振子中的大質量粒子的圖中，位置和動量算符可以用上面相同公式中的湮沒算子來表示，並用於計算方差， $\sigma _{x}^{2}={\frac {\hbar }{2m\omega }},$ $\sigma _{p}^{2}={\frac {\hbar m\omega }{2}}.$ 因此，每個相干態都飽和肯納德界 $\sigma _{x}\sigma _{p}={\sqrt {\frac {\hbar }{2m\omega }}}\,{\sqrt {\frac {\hbar m\omega }{2 }}}={\frac {\hbar }{2}}.$ 位置和動量各貢獻一定量 ${\textstyle {\sqrt {\hbar /2}}}$ 以“平衡”的方式。此外，儘管位置和動量的單獨貢獻一般不需要平衡，但每個壓縮相干態也飽和肯納德界。

盒子裡的顆粒

考慮一維長度盒子中的粒子 $L$ 。位置和動量空間的本徵函數是 $\psi _{n}(x,t)={\begin{cases}A\sin(k_{n}x)\mathrm {e} ^{-\mathrm {i} \omega _{n} t},&0<x<L,\\0,&{\text{否則,}}\end{案例}}$ 和 $\varphi _{n}(p,t)={\sqrt {\frac {\pi L}{\hbar }}}\,\,{\frac {n\left(1-(-1) ) ^{n}e^{-ikL}\right)e^{-i\omega _{n}t}}{\pi ^{2}n^{2}-k^{2}L^{2 } }},$ 在哪裡 ${\textstyle \omega _{n}={\frac {\pi ^{2}\hbar n^{2}}{8L^{2}m}}}$ 我們使用了德布羅意關係 $p=\hbar k$ 。的變異數為 $x$ 和 $p$ 可以明確計算： $\sigma _{x}^{2}={\frac {L^{2}}{12}}\left(1-{\frac {6}{n^{2}\pi ^{2 }}}\正確的）$ $\sigma _{p}^{2}=\left({\frac {\hbar n\pi }{L}}\right)^{2}.$

因此，標準差的乘積為 $\sigma _{x}\sigma _{p}={\frac {\hbar }{2}}{\sqrt {{\frac {n^{2}\pi ^{2}}{3} }-2}}.$ 對於所有人 $n=1,\,2,\,3,\,\ldots$ , 數量 ${\textstyle {\sqrt {{\frac {n^{2}\pi ^{2}}{3}}-2}}}$ 大於1，因此永遠不會違反不確定原理。對於數值具體而言，最小值出現在以下情況： $n=1$ ，在這種情況下 $\sigma _{x}\sigma _{p}={\frac {\hbar }{2}}{\sqrt {{\frac {\pi ^{2}}{3}}-2}} \約0.568\hbar >{\frac {\hbar }{2}}.$

動力源源不絕

假設粒子最初具有由圍繞某個恆定動量p ₀的常態分佈所描述的動量空間波函數，根據 $\varphi (p)=\left({\frac {x_{0}}{\hbar {\sqrt {\pi }}}}\right)^{1/2}\exp \left({\壓裂{-x_{0}^{2}(p-p_{0})^{2}}{2\hbar ^{2}}}\right),$ 我們引入了參考量表 ${\textstyle x_{0}={\sqrt {\hbar /m\omega _{0}}}}$ ，和 $\omega _{0}>0$ 描述分佈的寬度——請參閱。無量綱化。如果允許狀態在自由空間中演化，則與時間相關的動量和位置空間波函數為 $\Phi (p,t)=\left({\frac {x_{0}}{\hbar {\sqrt {\pi }}}}\right)^{1/2}\exp \left( {\frac {-x_{0}^{2}(p-p_{0})^{2}}{2\hbar ^{2}}}-{\frac {ip^{2}t}{2m \hbar }}\右),$ $\Psi (x,t)=\left({\frac {1}{x_{0}{\sqrt {\pi }}}}\right)^{1/2}{\frac {e^ {-x_{0}^{2}p_{0}^{2}/2\hbar ^{2}}}{\sqrt {1+i\omega _{0}t}}\,\exp \左(-{\frac {(x-ix_{0}^{2}p_{0}/\hbar )^{2}}{2x_{0}^{2}(1+i\omega _{0} t)}}\右).$

自從 $\langle p(t)\rangle =p_{0}$ 和 $\sigma _{p}(t)=\hbar /({\sqrt {2}}x_{0})$ ，這可以解釋為粒子以任意高精度沿著恆定動量移動。另一方面，位置的標準差是 $\sigma _{x}={\frac {x_{0}}{\sqrt {2}}}{\sqrt {1+\omega _{0}^{2}t^{2}}}$ 使得不確定性乘積只能隨著時間的推移而增加 $\sigma _{x}(t)\sigma _{p}(t)={\frac {\hbar }{2}}{\sqrt {1+\omega _{0}^{2}t ^{2}}}$

數學形式主義

從 Kennard 對位置動量不確定性的推導開始，Howard Percy Robertson發展了^[ 13 ]^[ 1 ]任意Hermitian 算子的公式 ${\hat {\mathcal {O}}}$ 以標準差表示 $\sigma _{\mathcal {O}}={\sqrt {\langle {\hat {\mathcal {O}}}^{2}\rangle -\langle {\hat {\mathcal {O}} }\rangle ^{2}}},$ 其中括號 $\langle {\hat {\mathcal {O}}}\rangle$ 表示由運算子表示的可觀察量的期望值 ${\hat {\mathcal {O}}}$ 。對於一對算子 ${\hat {A}}$ 和 ${\hat {B}}$ ，定義它們的換向器為 $[{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}} ,$

羅伯遜不確定性關係由^{[ 14 ]給出} $\sigma _{A}\sigma _{B}\geq \left|{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\ rangle \right|={\frac {1}{2}}\left|\langle [{\hat {A}},{\hat {B}}]\rangle \right|.$

Erwin Schrödinger ^[ 15 ]展示如何考慮算子之間的相關性，從而給出更強的不等式，稱為Robertson-Schrödinger 不確定性關係，^[ 16 ]^[ 1 ]

$\sigma _{A}^{2}\sigma _{B}^{2}\geq \left|{\frac {1}{2}}\langle \{{\hat {A}}, {\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \right|^{2}+\left|{\frac {1 }{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle \right|^{2},$

其中反換向器， $\{{\hat {A}},{\hat {B}}\}={\hat {A}}{\hat {B}}+{\hat {B}}{\hat {A }}$ 被使用。

薛丁格不確定關係的證明

這裡顯示的推導結合併建立在 Robertson、^[ 13 ] Schrödinger ^[ 16 ]和標準教科書（例如 Griffiths）中顯示的推導基礎上。^[ 17 ]^{: 138}對任何厄米算子 ${\hat {A}}$ ，根據方差的定義，我們有 $\sigma _{A}^{2}=\langle ({\hat {A}}-\langle {\hat {A}}\rangle )\Psi |({\hat {A}}-\ langle {\hat {A}}\rangle )\Psi \rangle .$ 我們讓 $|f\rangle =|({\hat {A}}-\langle {\hat {A}}\rangle )\Psi \rangle$ 因此 $\sigma _{A}^{2}=\langle f\mid f\rangle \,.$

類似地，對於任何其他埃爾米特算子 ${\hat {B}}$ 在同一個狀態下 $\sigma _{B}^{2}=\langle ({\hat {B}}-\langle {\hat {B}}\rangle )\Psi |({\hat {B}}-\ langle {\hat {B}}\rangle )\Psi \rangle =\langle g\mid g\rangle$ 為了 $|g\rangle =|({\hat {B}}-\langle {\hat {B}}\rangle )\Psi \rangle .$

兩個偏差的乘積因此可以表示為

\sigma _{A}^{2}\sigma _{B}^{2}=\langle f\mid f\rangle \langle g\mid g\rangle .

( 1 )

為了關聯兩個向量 $|f\rangle$ 和 $|g\rangle$ ，我們使用柯西-施瓦茲不等式^[ 18 ]，其定義為 $\langle f\mid f\rangle \langle g\mid g\rangle \geq |\langle f\mid g\rangle |^{2},$ 因此方程式( 1 )可以寫成

\sigma _{A}^{2}\sigma _{B}^{2}\geq |\langle f\mid g\rangle |^{2}.

( 2 )

自從 $\langle f\mid g\rangle$ 通常是一個複數，我們使用任何複數的模平方這一事實 $z$ 定義為 $|z|^{2}=zz^{*}$ ，在哪裡 $z^{*}$ 是複共軛 $z$ 。模的平方也可以表示為

|z|^{2}={\Big (}\operatorname {Re} (z){\Big )}^{2}+{\Big (}\operatorname {Im} (z){\Big )}^{2}={\Big (}{\frac {z+z^{\ast }}{2}}{\Big )}^{2}+{\Big (}{\frac {zz^ {\ast }}{2i}}{\大)}^{2}.

( 3 )

我們讓 $z=\langle f\mid g\rangle$ 和 $z^{*}=\langle g\mid f\rangle$ 並將這些代入上面的等式中得到

|\langle f\mid g\rangle |^{2}={\bigg (}{\frac {\langle f\mid g\rangle +\langle g\mid f\rangle }{2}}{ \bigg )}^{2}+{\bigg (}{\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}{\bigg )}^{2}

( 4 )

內積 $\langle f\mid g\rangle$ 明確寫為 $\langle f\mid g\rangle =\langle ({\hat {A}}-\langle {\hat {A}}\rangle )\Psi |({\hat {B}}-\langle { \hat {B}}\rangle )\Psi \rangle ,$ 並利用這一事實 ${\hat {A}}$ 和 ${\hat {B}}$ 是埃爾米特算子，我們發現 ${\begin{對齊}\langle f\mid g\rangle &=\langle \Psi |({\hat {A}}-\langle {\hat {A}}\rangle )({\hat { B}}-\langle {\hat {B}}\rangle )\Psi \rangle \\[4pt]&=\langle \Psi \mid ({\hat {A}}{\hat {B}}-{ \hat {A}}\langle {\hat {B}}\rangle -{\hat {B}}\langle {\hat {A}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle )\Psi \rangle \\[4pt]&=\langle \Psi \mid {\hat {A}}{\hat {B}}\Psi \rangle -\langle \Psi \mid {\hat {A}}\langle {\hat {B}}\rangle \Psi \rangle -\langle \Psi \mid {\hat {B}}\langle {\hat {A}}\rangle \ Psi \rangle +\langle \Psi \mid \langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \Psi \rangle \\[4pt]&=\langle {\hat {A }}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\帽子{B}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \\[4pt]&=\langle {\hat {A}}{\hat { B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle .\end{對齊}}$

類似地可以證明 $\langle g\mid f\rangle =\langle {\hat {B}}{\hat {A}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B} }\範圍.$

因此，我們有 $\langle f\mid g\rangle -\langle g\mid f\rangle =\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\ rangle \langle {\hat {B}}\rangle -\langle {\hat {B}}{\hat {A}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B }}\rangle =\langle [{\hat {A}},{\hat {B}}]\rangle$ 和 $\langle f\mid g\rangle +\langle g\mid f\rangle =\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\ rangle \langle {\hat {B}}\rangle +\langle {\hat {B}}{\hat {A}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B }}\rangle =\langle \{{\hat {A}},{\hat {B}}\}\rangle -2\langle {\hat {A}}\rangle \langle {\hat {B}} \ 角.$

我們現在將上面的兩個方程式代回方程式。 ( 4 ) 並得到 $|\langle f\mid g\rangle |^{2}={\Big (}{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B }}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle {\Big )}^{2}+{\Big (}{\frac {1} {2i}}\langle [{\hat {A}},{\hat {B}}]\rangle {\Big )}^{2}\,.$

將上式代入式( 2 )可得薛丁格不確定關係 $\sigma _{A}\sigma _{B}\geq {\sqrt {{\Big (}{\frac {1}{2}}\langle \{{\hat {A}},{\帽子{B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle {\Big )}^{2}+{\Big (}{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle {\Big )}^{2}}}.$

此證明存在一個與所涉及的運算符的域相關的問題^[ 19 ] 。為了使證明有意義，向量 ${\hat {B}}|\Psi \rangle$ 必須在無界運算符的域內 ${\hat {A}}$ ，情況並非總是如此。事實上，羅伯遜不確定性關係是錯誤的，如果 ${\hat {A}}$ 是一個角度變數並且 ${\hat {B}}$ 是關於該變數的導數。在這個例子中，換向器是一個非零常數——就像海森堡不確定性關係一樣——但也存在著不確定性乘積為零的狀態。^[ 20 ]（請參閱下面的反例部分。）可以透過使用變分方法來證明，^[ 21 ]^[ 22 ]或透過使用規範交換關係的指數版本來克服這個問題。^[ 20 ]

請注意，在羅伯遜-薛丁格不確定性關係的一般形式中，無需假設算子 ${\hat {A}}$ 和 ${\hat {B}}$ 是自伴算子.假設它們只是對稱運算子就足夠了。（這兩個概念之間的區別通常在物理文獻中被掩蓋，其中術語Hermitian用於任一類或兩類算子。有關這一重要但技術性區別的詳細討論，請參閱 Hall 的書^[ 23 ]的第9 章。

相空間

在量子力學的相空間公式中，羅伯遜-薛丁格關係是由實星方函數的正性條件得出。給定一個維格納函數 $W(x,p)$ 對於明星產品★ 和函數f，以下情況通常是正確的：^[ 24 ] $\langle f^{*}\star f\rangle =\int (f^{*}\star f)\,W(x,p)\,dx\,dp\geq 0~.$

選擇 $f=a+bx+cp$ ，我們到達 $\langle f^{*}\star f\rangle ={\begin{bmatrix}a^{*}&b^{*}&c^{*}\end{bmatrix}}{\begin{bmatrix}1& \langle x\rangle &\langle p\rangle \\\langle x\rangle &\langle x\star x\rangle &\langle x\star p\rangle \\\langle p\rangle &\langle p\star x \rangle &\langle p\star p\rangle \end{bmatrix}}{\begin{bmatrix}a\\b\\c\end{bmatrix}}\geq 0~.$

由於此正性條件對於所有 a、b和c均成立，因此矩陣的所有特徵值都是非負的。

非負特徵值則意味著行列式上對應的非負條件， $\det {\begin{bmatrix}1&\langle x\rangle &\langle p\rangle \\\langle x\rangle &\langle x\star x\rangle &\langle x\star p\rangle \\ \langle p\rangle &\langle p\star x\rangle &\langle p\star p\rangle \end{bmatrix}}=\det {\begin{bmatrix}1&\langle x\rangle &\langle p\rangle \\\langle x\rangle &\langle x^{2}\rangle &\left\langle xp+{\frac {i\hbar }{2}}\right\rangle \\\langle p\rangle &\left\ langle xp-{\frac {i\hbar }{2}}\right\rangle &\langle p^{2}\rangle \end{bmatrix}}\geq 0~,$ 或者，明確地，在代數運算之後， $\sigma _{x}^{2}\sigma _{p}^{2}=\left(\langle x^{2}\rangle -\langle x\rangle ^{2}\right)\左(\langle p^{2}\rangle -\langle p\rangle ^{2}\right)\geq \left(\langle xp\rangle -\langle x\rangle \langle p\rangle \right)^{ 2}+{\frac {\hbar ^{2}}{4}}~.$

範例

由於羅伯遜和薛丁格關係適用於一般算子，因此可以將這些關係應用於任兩個可觀測量以獲得特定的不確定性關係。下面給出了文獻中發現的一些最常見的關係。

位置-線性動量不確定關係：對於位置和線性動量算子，規範交換關係 $[{\hat {x}},{\hat {p}}]=i\hbar$ 隱含了上面的肯納德不等式： $\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}.$
角動量不確定關係：對於物體總角動量算符的兩個正交分量： $\sigma _{J_{i}}\sigma _{J_{j}}\geq {\frac {\hbar }{2}}{\big |}\langle J_{k}\rangle {\big |},$ 其中i、j、k不同，J _i表示沿x _i軸的角動量。這種關係意味著，除非所有三個分量一起消失，否則只能以任意精度定義系統角動量的單一分量，通常是與外部（磁場或電場）平行的分量。此外，對於 $[J_{x},J_{y}]=i\hbar \varepsilon _{xyz}J_{z}$ , 一個選擇 ${\hat {A}}=J_{x}$ , ${\hat {B}}=J_{y}$ ，在角動量多重態中，ψ = | j , m ⟩，限制卡西米爾不變量（角動量平方， $\langle J_{x}^{2}+J_{y}^{2}+J_{z}^{2}\rangle$ ) 從下面產生有用的約束，例如j ( j + 1) ≥ m ( m + 1)，因此j ≥ m等等。

對於超導體中的電子數量及其Ginzburg-Landau 序參數的相位^[²⁵^]^[²⁶^] $\Delta N\,\Delta \varphi \geq 1.$

限制

算子羅伯遜不等式的推導 ${\hat {A}}$ 和 ${\hat {B}}$ 需要 ${\hat {A}}{\hat {B}}\psi$ 和 ${\hat {B}}{\hat {A}}\psi$ 待定義。在某些量子系統中，這些條件不成立。^[ 27 ]一個例子是環上的量子粒子，其中波函數取決於角度變數。 $\theta$ 在區間內 $[0,2\pi ]$ 。定義“位置”和“動量”運算符 ${\hat {A}}$ 和 ${\hat {B}}$ 經過 ${\hat {A}}\psi (\theta )=\theta \psi (\theta ),\quad \theta \in [0,2\pi ],$ 和 ${\hat {B}}\psi =-i\hbar {\frac {d\psi }{d\theta }},$ 具有周期性邊界條件 ${\hat {B}}$ 。的定義 ${\hat {A}}$ 取決於 $\theta$ 範圍從 0 到 $2\pi$ 。這些算子滿足位置和動量算符的通常交換關係， $[{\hat {A}},{\hat {B}}]=i\hbar$ 。更準確地說， ${\hat {A}}{\hat {B}}\psi -{\hat {B}}{\hat {A}}\psi =i\hbar \psi$ 每當兩者 ${\hat {A}}{\hat {B}}\psi$ 和 ${\hat {B}}{\hat {A}}\psi$ 被定義，並且這樣的空間 $\psi$ 是量子希爾伯特空間的稠密子空間。^[ 28 ]

現在讓 $\psi$ 是任何本徵態 ${\hat {B}}$ ，由下式給出 $\psi (\theta )=e^{2\pi in\theta }$ 。與線上動量算符的本徵態不同，這些狀態是可歸一化的。還有營運商 ${\hat {A}}$ 是有界的，因為 $\theta$ 範圍在有界區間內。因此，在該狀態 $\psi$ ，不確定性 $B$ 為零且不確定性 $A$ 是有限的，因此 $\sigma _{A}\sigma _{B}=0.$ 羅伯遜不確定性原理在這種情況下不適用： $\psi$ 不在營運商的管轄範圍內 ${\hat {B}}{\hat {A}}$ ，因為乘以 $\theta$ 破壞施加於的周期性邊界條件 ${\hat {B}}$ 。^[ 20 ]

對於通常的位置和動量算子 ${\hat {X}}$ 和 ${\hat {P}}$ 在實線上，不可能出現這樣的反例。只要 $\sigma _{x}$ 和 $\sigma _{p}$ 在狀態中定義 $\psi$ ，海森堡測不準原理成立，即使 $\psi$ 未能在域內 ${\hat {X}}{\hat {P}}$ 或的 ${\hat {P}}{\hat {X}}$ 。^[ 29 ]

混合狀態

羅伯遜-薛丁格不確定性可以改善，因為它必須適用於所有組件 $\varrho _{k}$ 在密度矩陣的任何分解中，給出如下 $\varrho =\sum _{k}p_{k}\varrho _{k}.$ 在這裡，對於機率 $p_{k}\geq 0$ 和 $\sum _{k}p_{k}=1$ 抓住。然後，利用關係式 $\sum _{k}a_{k}\sum _{k}b_{k}\geq \left(\sum _{k}{\sqrt {a_{k}b_{k}}}\right )^{2}$ 為了 $a_{k},b_{k}\geq 0$ ，由此可知^[ 30 ] $\sigma _{A}^{2}\sigma _{B}^{2}\geq \left[\sum _{k}p_{k}L(\varrho _{k})\right] ^{2},$ 定義邊界中的函數的位置 $L(\varrho )={\sqrt {\left|{\frac {1}{2}}\operatorname {tr} (\rho \{A,B\})-\operatorname {tr} (\ rho A)\運算子名稱{tr} (\rho B)\right|^{2}+\left|{\frac {1}{2i}}\運算子名稱{tr} (\rho [A,B ])\right |^{2}}}.$ 上述關係的界限通常大於原始羅伯遜-薛定諤不確定關係的界限。因此，我們需要計算量子態混合分量而不是量子態的羅伯遜-薛丁格不確定性的界限，並計算它們的平方根的平均值。以下表達式比 Robertson-Schrödinger 不確定性關係更強 $\sigma _{A}^{2}\sigma _{B}^{2}\geq \left[\max _{p_{k},\varrho _{k}}\sum _{k} p_{k}L(\varrho _{k})\right]^{2},$ 在右側，密度矩陣的分解上方有一個凹形屋頂。上述改進的關係被所有單量子位元量子態飽和。^[ 30 ]

透過類似的論證，我們可以推導出與右側凸屋頂的關係^[ 30 ] $\sigma _{A}^{2}F_{Q}[\varrho ,B]\geq 4\left[\min _{p_{k},\Psi _{k}}\sum _{k }p_{k}L(\vert \Psi _{k}\rangle \langle \Psi _{k}\vert )\right]^{2}$ 在哪裡 $F_{Q}[\varrho ,B]$ 表示量子費希爾訊息，密度矩陣分解為純態： $\varrho =\sum _{k}p_{k}\vert \Psi _{k}\rangle \langle \Psi _{k}\vert .$ 該推導利用了量子費希爾資訊是方差乘以四的凸屋頂這一事實。 ^[ 31 ]^[ 32 ]

沒有凸屋頂的更簡單的不等式如下^[ 33 ] $\sigma _{A}^{2}F_{Q}[\varrho ,B]\geq \vert \langle i[A,B]\rangle \vert ^{2},$ 這比海森堡不確定性關係更強，因為對於量子費希爾訊息，我們有 $F_{Q}[\varrho ,B]\leq 4\sigma _{B},$ 而對純粹國家來說，平等成立。

Maccone-Pati 不確定性關係

如果系統的狀態被選擇為可觀測量之一的本徵態，則羅伯遜-薛丁格不確定性關係可能是微不足道的。 Lorenzo Maccone 和Arun K. Pati證明的更強的不確定性關係給出了兩個不相容的可觀測量的變異總和的非平凡界限。^[ 34 ]（早期關於將不確定性關係公式化為方差之和的工作包括，例如 Yichen Huang 的參考文獻^[ 35 ]。）對於兩個非通勤可觀測量 $A$ 和 $B$ 第一個更強的不確定性關係由下式給出 $\sigma _{A}^{2}+\sigma _{B}^{2}\geq \pm i\langle \Psi \mid [A,B]|\Psi \rangle +\mid \langle \Psi \mid (A\pm iB)\mid {\bar {\Psi }}\rangle |^{2},$ 在哪裡 $\sigma _{A}^{2}=\langle \Psi |A^{2}|\Psi \rangle -\langle \Psi \mid A\mid \Psi \rangle ^{2}$ , $\sigma _{B}^{2}=\langle \Psi |B^{2}|\Psi \rangle -\langle \Psi \mid B\mid \Psi \rangle ^{2}$ , $|{\bar {\Psi }}\rangle$ 是與系統狀態正交的歸一化向量 $|\Psi \rangle$ 並且應該選擇的符號 $\pm i\langle \Psi \mid [A,B]\mid \Psi \rangle$ 使這個實際數量成為正數。

第二個更強的不確定性關係由下式給出 $\sigma _{A}^{2}+\sigma _{B}^{2}\geq {\frac {1}{2}}|\langle {\bar {\Psi }}_{A +B}\mid (A+B)\mid \Psi \rangle |^{2}$ 在哪裡 $|{\bar {\Psi }}_{A+B}\rangle$ 是正交狀態 $|\Psi \rangle$ 。形式為 $|{\bar {\Psi }}_{A+B}\rangle$ 意味著新的不確定性關係的右側不為零，除非 $|\Psi \rangle$ 是一個本徵態 $(A+B)$ 。人們可能會注意到 $|\Psi \rangle$ 可以是一個本徵態 $(A+B)$ 不是任何一個的本徵態 $A$ 或者 $B$ 。然而，當 $|\Psi \rangle$ 是兩個可觀測量之一的本徵態，海森堡-薛丁格不確定性關係變得微不足道。但新關係中的下界不為零，除非 $|\Psi \rangle$ 是兩者的本徵態。

能量-時間

能量-時間不確定性關係如 $\Delta E\Delta t\gtrsim \hbar /2,$ 有著悠久且有爭議的歷史；的意義 $\Delta t$ 和 $\Delta E$ 各不相同，不同的表述具有不同的有效性領域。^[ 36 ]然而，一個眾所周知的應用既已得到充分確立^[ 37 ]^[ 38 ]並經過實驗驗證：^[ 39 ]^[ 40 ]共振態壽命之間的聯繫， $\tau _{\sqrt {1/2}}$ 及其能量寬度 $\Delta E$ : $\tau _{\sqrt {1/2}}\Delta E=\pi \hbar /4.$ 在粒子物理學中，實驗擬合到布賴特-維格納能量分佈的寬度用於表徵準穩定或衰變狀態的壽命。^[ 41 ]

此原理的非正式、啟發式意義如下：^[ 42 ]僅存在很短時間的狀態不能具有確定的能量。為了具有確定的能量，必須準確定義狀態的頻率，這要求狀態停留許多週期，這是所需精度的倒數。例如，在光譜學中，激發態的壽命是有限的。根據時間-能量不確定性原理，它們沒有確定的能量，並且每次衰變時釋放的能量略有不同。出射光子的平均能量在該態的理論能量處有一個峰值，但分佈具有有限的寬度，稱為自然線寬。快衰減態具有寬線寬，而慢衰減態具有窄線寬。^[ 43 ]同樣的線寬效應也使得在粒子物理學中指定不穩定、快速衰變粒子的剩餘質量變得困難。粒子衰變越快（其壽命越短），其質量就越不確定（粒子的寬度越大）。

量子力學中的時間

量子力學中的「時間」概念提出了許多挑戰。^[ 44 ]不存在時間測量的量子理論；相對論既是時間的基礎，又很難包含在量子力學中。^[ 36 ]雖然位置和動量與單一粒子相關，但時間是一個系統屬性：它不需要羅伯遜-薛丁格關係所需的算符。^[ 1 ]穩定性和不穩定量子系統的數學處理不同。^[ 45 ]這些因素結合起來使能量-時間不確定性原則引起爭議。

「時間」可分為三個概念：^[ 36 ]外在的、內在的、可觀察的。外部或實驗室時間由實驗者看到；內在時間是透過動態變數的變化來推斷的，例如鐘錶的指標或自由粒子的運動；可觀察時間涉及作為可觀察的時間，即時間間隔事件的測量。

外在時間能量-時間不確定原理可能會說，以精確度測量量子系統的能量 $\Delta E$ 需要一個時間間隔 $\Delta t>h/\Delta E$ 。^[ 38 ]然而，Yakir Aharonov和David Bohm ^[ 46 ]^[ 36 ]表明，在某些量子系統中，可以在任意短的時間內精確測量能量：外部時間不確定性原理並不普遍。

固有時間是多種能量-時間不確定性關係公式的基礎，包括下一節討論的曼德爾斯坦-塔姆關係。具有與外部實驗室時間緊密匹配的內在時間的物理系統稱為“時鐘”。^[ 44 ]^：31

可觀測時間，測量兩個事件之間的時間，仍然是量子理論的挑戰。採用積極的運營商重視措施概念已取得一些進展。^[ 36 ]

曼德爾施塔姆-塔姆

1945 年，Leonid Mandelstam和Igor Tamm推導出非相對論時間-能量不確定關係如下。^[ 47 ]^[ 36 ]根據海森堡力學，無顯式時間依賴性的可觀測B的廣義Ehrenfest 定理，由自伴算子表示 ${\hat {B}}$ 涉及平均值的時間依賴性 ${\hat {B}}$ 以其換向器與哈密頓量的平均值：

${\frac {d\langle {\hat {B}}\rangle }{dt}}={\frac {i}{\hbar }}\langle [{\hat {H}},{\hat {B}}]\rangle .$

的價值 $\langle [{\hat {H}},{\hat {B}}]\rangle$ 然後代入羅伯遜不確定性關係中的能量算子 ${\hat {H}}$ 和 ${\hat {B}}$ : $\sigma _{H}\sigma _{B}\geq \left|{\frac {1}{2i}}\langle [{\hat {H}},{\hat {B}}]\範圍\right|,$ 給予 $\sigma _{H}{\frac {\sigma _{B}}{\left|{\frac {d\langle {\hat {B}}\rangle }{dt}}\right|}} \geq {\frac {\hbar }{2}}$ （只要分母非零）。雖然這是一個普遍的結果，但它取決於所選的可觀察結果以及偏差 $\sigma _{H}$ 和 $\sigma _{B}$ 是針對特定狀態計算的。識別 $\Delta E\equiv \sigma _{E}$ 和特徵時間 $\tau _{B}\equiv {\frac {\sigma _{B}}{\left|{\frac {d\langle {\hat {B}}\rangle }{dt}}\right| }}$ 給出能量-時間關係 $\Delta E\tau _{B}\geq {\frac {\hbar }{2}}.$ 雖然 $\tau _{B}$ 具有時間的維度，與進入薛丁格方程式的時間參數t不同。這 $\tau _{B}$ 可以解釋為可觀測值的期望值的時間， $\langle {\hat {B}}\rangle ,$ 變化量等於一個標準差。^[ 48 ] 範例：

自由量子粒子透過空間中一點的時間更加不確定，因為狀態能量受到更精確的控制： $\Delta T=\hbar /2\Delta E.$ 由於時間擴散與粒子位置擴散有關，能量擴散與動量擴散有關，因此這種關係與位置動量不確定性直接相關。^[ 17 ]^：144
Delta粒子是與質子和中子有關的夸克的準穩定複合物，其壽命為10 ^-23 s，因此其測得的相當於能量的質量1232 MeV/ c ²變化±120 MeV/ c ²；這種變化是固有的，不是由測量誤差引起的。^[ 17 ]^：144
兩種能量狀態 $\psi _{1,2}$ 有能量 $E_{1,2},$ 疊加以建立複合狀態

{\displaystyle \Psi (x,t)=a\psi _{1}(x)e^{-iE_{1}t/h}+b\psi _{2}(x)e^{-iE_{ 2}噸/小時}。

此狀態的機率幅度有一個與時間相關的干擾項：

|\Psi (x,t)|^{2}=a^{2}|\psi _{1}(x)|^{2}+b^{2}|\psi _{2} (x)|^{2}+2ab\cos({\frac {E_{2}-E_{1}}{\hbar }}t).

振盪週期與能量差成反比：

\tau =2\pi \hbar /(E_{2}-E_{1})

。^[ 17 ]^：144

根據所使用的可觀測值和狀態，每個範例對於時間不確定性都有不同的意義。

量子場論

量子場論的一些公式在其計算中使用稱為虛粒子的臨時電子-正電子對。這些粒子的質能和壽命透過能量-時間不確定性關係相關。量子系統的能量尚不足夠精確，無法將其行為限制在單一、簡單的歷史範圍內。因此，所有歷史的影響都必須納入量子計算中，包括那些能量比測量/計算的能量分佈平均值大得多或少得多的歷史。

能量-時間不確定原理暫時不違反能量守恆定律；並不代表可以從宇宙中「借」能量，只要在短時間內「歸還」能量即可。^[ 17 ]^{: 145}宇宙的能量並非總是一個確切已知的參數。^[ 1 ]當事件以非常短的時間間隔發生時，這些事件的能量存在不確定性。

諧波分析

在調和分析的背景下，不確定性原理意味著人們不能同時定位函數及其傅立葉變換的值。也就是說，以下不等式成立， $\left(\int _{-\infty }^{\infty }x^{2}|f(x)|^{2}\,dx\right)\left(\int _{-\infty }x^{2}|f(x)|^{2}\,dx\right)\left(\int _{-\infty }^{\infty }\xi ^{2}|{\hat {f }}(\xi )|^{2}\,d\xi \right)\geq {\frac {\|f\|_{ 2}^{4}}{16\pi ^{2}}}.$

進一步的數學不確定性不等式，包括上述熵不確定性，在函數 $f$ 及其傅立葉轉換 $f̂$ 之間成立：^[ 49 ]^[ 50 ]^[ 51 ] $H_{x}+H_{\xi }\geq \log(e/2)$

訊號處理

在時頻分析中，不確定性原理稱為Gabor 極限（以Dennis Gabor命名），有時稱為Heisenberg-Gabor 極限。從下面的「貝尼迪克斯定理」得出的基本結果是，函數不能同時受時間限制和頻帶限制（函數及其傅立葉變換不能同時具有有界域） - 請參閱頻帶限制與時間限制。更準確地說，時間頻寬或持續時間頻寬乘積滿足 $\sigma _{t}\sigma _{f}\geq {\frac {1}{4\pi }}\約 0.08{\text{ 週期}},$ 在哪裡 $\sigma _{t}$ 和 $\sigma _{f}$ 分別是時間和頻率能量濃度的標準差。^[ 52 ]對於高斯形脈衝（Gabor小波）獲得最小值[對於非平方高斯（即訊號幅度）及其非平方傅立葉變換幅度 $\sigma _{t}\sigma _{f}=1/2\pi$ ;平方減少了每個 $\西格瑪$ 由一個因素 ${\sqrt {2}}$ .] 另一種常見的測量方法是（功率/能量）半高時間和頻率全寬的乘積，對於高斯來說等於 $2\ln 2/\pi \約 0.44$ （請參閱頻寬限制脈衝）。

換句話說，人們不能同時在時域和頻域中清晰地定位訊號 $f$ 。

當應用於濾波器時，結果意味著無法同時實現高時間分辨率和高頻分辨率；一個具體的例子是短時傅立葉變換的分辨率問題——如果使用寬窗口，則以犧牲時間分辨率為代價獲得良好的頻率分辨率，而窄窗口則具有相反的權衡。

替代定理給出了更精確的定量結果，並且在時頻分析中，不是單獨解釋（1 維）時域和頻域，而是將極限解釋為（2 維）中函數的支持下限。時間-頻率平面。在實踐中，Gabor 極限限制了在沒有乾擾的情況下可以實現的同時時頻分辨率；可以實現更高的分辨率，但代價是訊號的不同分量相互幹擾。

因此，為了分析瞬態很重要的訊號，通常會使用小波轉換來取代傅立葉變換。

離散傅立葉變換

讓 $\left\{\mathbf {x_{n}} \right\}:=x_{0},x_{1},\ldots ,x_{N-1}$ 是一個由N 個複數組成的序列，並且 $\left\{\mathbf {X_{k}} \right\}:=X_{0},X_{1},\ldots ,X_{N-1},$ 是它的離散傅立葉變換。

表示為 $\|x\|_{0}$ 時間序列中非零元素的數量 $x_{0},x_{1},\ldots ,x_{N-1}$ 並由 $\|X\|_{0}$ 頻率序列中非零元素的數量 $X_{0},X_{1},\ldots ,X_{N-1}$ 。然後， $\|x\|_{0}\cdot \|X\|_{0}\geq N.$

這種不等式是尖銳的，當x或X是狄拉克質量時，或者更一般地，當x是在整數模N的子群上支持的狄拉克梳的非零倍數時（在這種情況下，X也是支持狄拉克梳的），就可以實現等式。

更一般地，如果T和W是整數模N的子集，令 $L_{T},R_{W}:\ell ^{2}(\mathbb {Z} /N\mathbb {Z} )\to \ell ^{2}(\mathbb {Z} /N\ mathbb {Z} )$ 分別表示時間限制運算子和頻寬限制運算子。然後 $\|L_{T}R_{W}\|^{2}\leq {\frac {|T||W|}{|G|}}$ 其中範數是希爾伯特空間上算子的算子範數 $\ell ^{2}(\mathbb {Z} /N\mathbb {Z} )$ 整數模N上的函數。這種不等式對訊號重建有影響。^[ 53 ]

當N是質數時，更強的不等式成立： $\|x\|_{0}+\|X\|_{0}\geq N+1.$ 陶哲軒發現，這種不平等也是尖銳的。^[ 54 ]

貝尼迪克斯定理

Amrein–Berthier ^[ 55 ]和 Benedicks 定理^[ 56 ] $直觀地表明， f$ 非零的點集和 $f̂$ 非零的點集不能都很小。

$具體來說， L$ $2$ $($ $R$ $)$ 中的函數 $f$ 及其傅立葉變換 $f̂$ 不可能同時支援有限勒貝格測度集。更定量的版本是^[⁵⁷^]^[⁵⁸^] $\|f\|_{L^{2}(\mathbf {R} ^{d})}\leq Ce^{C|S||\Sigma |}{\bigl (}\|f\ |_{L^{2}(S^{c})}+\|{\hat {f}}\|_{L^{2}(\Sigma ^{c})}{\bigr )}~ .$

人們期望因子 $Ce C | S || Σ |可以用$ $Ce C (| S || Σ |) 1/ d$ 代替，只有當 $S$ 或 $Σ$ 是凸的時才知道。

哈代測不準原理

數學家GH Hardy提出了以下不確定性原理：^[ 59 ] $f$ 和 $f̂$ 不可能同時「非常快速地減少」。具體來說，如果 $f$ 在 $L^{2}(\mathbb {R} )$ 是這樣的 $|f(x)|\leq C(1+|x|)^{N}e^{-a\pi x^{2}}$ 和 $|{\hat {f}}(\xi )|\leq C(1+|\xi |)^{N}e^{-b\pi \xi ^{2}}$ （ $C>0,N$ 一個整數），那麼，如果 $ab > 1， f = 0$ ，而如果 $ab = 1$ ，則存在一個次數 $\leq$ $N$ 的多項式 $P$ 使得 $f(x)=P(x)e^{-a\pi x^{2}}.$

後來對此進行了改進，如下：如果 $f\in L^{2}(\mathbb {R} ^{d})$ 是這樣的 $\int _{\mathbb {R} ^{d}}\int _{\mathbb {R} ^{d}}|f(x)||{\hat {f}}(\xi )| {\frac {e^{\pi |\langle x,\xi \rangle |}}{(1+|x|+|\xi |)^{N}}}\,dx\,d\xi <+ \infty ~,$ 然後 $f(x)=P(x)e^{-\pi \langle Ax,x\rangle }~,$ 其中 $P是$ $(N - d)/2$ 次多項式， $A$ 是實數 $d \times d$ 正定矩陣。

這一結果在 Beurling 的全集中沒有證明的情況下得到了闡述，並在 Hörmander ^[ 60 ]中得到了證明（案例 $d=1,N=0$ ）以及 Bonami、Demange 和 Jaming ^[ 61 ]對於一般情況。請注意，Hörmander–Beurling 的版本暗示了哈代定理中 $ab > 1 的$ 情況，而 Bonami–Demange–Jaming 的版本則涵蓋了哈代定理的全部優勢。基於劉維爾定理的伯林定理的不同證明出現在參考文獻中。^[ 62 ]

案例 $ab < 1$ 的完整描述以及以下對 Schwartz 類別分佈的擴展出現在參考文獻中。^[ 63 ]

定理 — 如果是緩和分佈 $f\in {\mathcal {S}}'(\mathbb {R} ^{d})$ 是這樣的 $e^{\pi |x|^{2}}f\in {\mathcal {S}}'(\mathbb {R} ^{d})$ 和 $e^{\pi |\xi |^{2}}{\hat {f}}\in {\mathcal {S}}'(\mathbb {R} ^{d})~,$ 然後 $f(x)=P(x)e^{-\pi \langle Ax,x\rangle }~,$ 對於一些方便的多項式 $P和$ $d$ $\times$ $d$ 類型的實數正定矩陣 $A$ 。

附加不確定性關係

海森堡極限

在量子計量學，特別是乾涉測量學中，海森堡極限是測量精度隨測量中使用的能量而變化的最佳速率。通常，這是相位的測量（應用於分束器的一個臂），能量由干涉儀中使用的光子數給出。儘管有人聲稱已經突破了海森堡極限，但這反映了對縮放資源定義的分歧。^[ 64 ]如果定義得當，海森堡極限是量子力學基本原理的結果，並且無法被打破，儘管弱海森堡極限是可以被打破的。^[ 65 ]

系統和統計錯誤

上述不等式集中於透過標準差量化的可觀測值的統計不精確性 $\西格瑪$ 。然而，海森堡的原始版本是在處理系統誤差，即測量儀器對量子系統的干擾，即觀察者效應。

如果我們讓 $\varepsilon _{A}$ 表示可觀測A的測量誤差（即不準確度），且 $\eta _{B}$ 先前測量A對共軛變數B的後續測量所產生的干擾，則 Masanao Ozawa 提出的不等式 - 包括系統誤差和統計誤差 - 成立：^[⁶⁶^]

$\varepsilon _{A}\,\eta _{B}+\varepsilon _{A}\,\sigma _{B}+\sigma _{A}\,\eta _{B}\,\ geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{ \更大\rangle }\right|$

海森堡的不確定性原理最初在 1927 年的表述中描述，僅提到了小澤不等式的第一項，即係統誤差。使用上面的符號來描述順序測量的誤差/幹擾效應（首先是A，然後是B），可以寫為

$\varepsilon _{A}\,\eta _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{ \hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

海森堡關係的形式推導是可能的，但遠非直觀。它不是由海森堡提出的，只是近年來才以數學上一致的方式表達出來。^[ 67 ]^[ 68 ] 另外，必須強調的是，海森堡公式沒有考慮到固有的統計誤差 $\sigma _{A}$ 和 $\sigma _{B}$ 。越來越多的實驗證據^[ 69 ]^[ 70 ]^[ 71 ]^[ 72 ]顯示總的量子不確定性不能單獨用海森堡項來描述，而是需要小澤不等式的所有三個項都存在。

使用相同的形式，^[ 1 ]還可以引入另一種物理情況，通常與前一種情況混淆，即同時測量的情況（A和B同時）：

$\varepsilon _{A}\,\varepsilon _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{ \hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

A和B上的兩個同時測量結果必然^[ 73 ] 不清晰或較弱。

也可以導出一種不確定性關係，就像小澤的不確定性關係一樣，結合了統計和系統誤差分量，但保持了非常接近海森堡原始不等式的形式。透過添加羅伯遜^[ 1 ]

$\sigma _{A}\,\sigma _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{ \hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

和小澤關係我們得到 $\varepsilon _{A}\eta _{B}+\varepsilon _{A}\,\sigma _{B}+\sigma _{A}\,\eta _{B}+\sigma _{ A}\sigma _{B}\geq \left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle } \右|.$ 這四個項可以寫成： $(\varepsilon _{A}+\sigma _{A})\,(\eta _{B}+\sigma _{B})\,\geq \,\left|{\Bigl \langle } {\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|.$ 定義： ${\bar {\varepsilon }}_{A}\,\equiv \,(\varepsilon _{A}+\sigma _{A})$ 作為變數A和的測量值的不準確度 ${\bar {\eta }}_{B}\,\equiv \,(\eta _{B}+\sigma _{B})$ 由於共軛變數B的波動，Kazuo Fujikawa ^[⁷⁴^]建立了一種類似海森堡原始關係的不確定性關係，但對於系統誤差和統計誤差都有效：

${\bar {\varepsilon }}_{A}\,{\bar {\eta }}_{B}\,\geq \,\left|{\Bigl \langle }{\bigl [}{ \hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

量子熵不確定原理

對於許多分佈來說，標準差並不是一種特別自然的量化結構的方式。例如，其中一個可觀測量是角度的不確定性關係對於大於一個週期的波動幾乎沒有物理意義。^[ 22 ]^[ 75 ]^[ 76 ]^[ 77 ]其他例子包括高度雙峰分佈或具有發散變異數的單峰分佈。

克服這些問題的解決方案是基於熵不確定性而不是方差乘積的不確定性。1957 年，休·埃弗雷特三世 (Hugh Everett III)在闡述量子力學的多世界解釋時，猜想了基於熵確定性的不確定性原理的更強擴展。^[⁷⁸^]這個猜想也由 II Hirschman ^[⁷⁹^]研究，並於 1975 年由 W. Beckner ^[⁸⁰^]以及 Iwo Bialynicki-Birula 和 Jerzy Mycielski ^[⁸¹^]證明，對於兩個歸一化、無量綱傅立葉變換對 $f$ $($ $a$ $)$ 和 $g$ $($ $b$ $)$ 其中

f(a)=\int _{-\infty }^{\infty }g(b)\ e^{2\pi iab}\,db

和

\,\,\,g(b)=\int _{-\infty }^{\infty }f(a)\ e^{-2\pi iab}\,da

香農資訊熵 $H_{a}=-\int _{-\infty }^{\infty }|f(a)|^{2}\log |f(a)|^{2}\,da,$ 和 $H_{b}=-\int _{-\infty }^{\infty }|g(b)|^{2}\log |g(b)|^{2}\,db$ 受到以下約束，

$H_{a}+H_{b}\geq \log(e/2)$

其中對數可以是任何底數。

$與位置波函數ψ (x)$ 和動量波函數 $ψ (x)$ 相關的機率分佈函數分別具有長度和動量的倒數維數，但熵可以透過以下方式呈現無量綱： $H_{x}=-\int |\psi (x)|^{2}\ln \left(x_{0}\,|\psi (x)|^{2}\right)dx=- \left\langle \ln \left(x_{0}\,\left|\psi (x)\right|^{2}\right)\right\rangle$ $H_{p}=-\int |\varphi (p)|^{2}\ln(p_{0}\,|\varphi (p)|^{2})\,dp=-\left \langle \ln(p_{0}\left|\varphi (p)\right|^{2})\right\rangle$ 其中 $x 0$ 和 $p 0$ 分別是任意選擇的長度和動量，這使得對數的參數無量綱。請注意，熵將是這些所選參數的函數。由於位置波函數 $ψ$ $($ $x$ $)$ 和動量波函數 $φ$ $($ $p$ $)之間的$ 傅立葉變換關係，對於對應的熵，上述約束可以寫為

$H_{x}+H_{p}\geq \log \left({\frac {e\,h}{2\,x_{0}\,p_{0}}}\right)$

其中 $h$ 是普朗克常數。

根據 $x 0 p 0$ 乘積的選擇，表達式可以用多種方式寫。如果選擇 $x 0 p 0$ 為 $h$ ，則 $H_{x}+H_{p}\geq \log \left({\frac {e}{2}}\right)$

相反，如果選擇 $x 0 p 0$ $為ħ$ ，則 $H_{x}+H_{p}\geq \log(e\,\pi )$

如果 $x 0$ 和 $p 0$ 在使用的任何單位制中選擇為統一，則 $H_{x}+H_{p}\geq \log \left({\frac {e\,h}{2}}\right)$ 其中 $h$ 被解釋為無量綱數，等於所選單位制中普朗克常數的值。請注意，這些不等式可以擴展到多模量子態，或多於一個空間維度的波函數。^[ 82 ]

量子熵不確定原理比海森堡不確定原理更具限制性。來自反對數 Sobolev 不等式^[ 83 ] $H_{x}\leq {\frac {1}{2}}\log(2e\pi \sigma _{x}^{2}/x_{0}^{2})~,$ $H_{p}\leq {\frac {1}{2}}\log(2e\pi \sigma _{p}^{2}/p_{0}^{2})~,$ （同樣地，從正態分佈在給定方差的情況下最大化所有此類分佈的熵這一事實），很容易得出這種熵不確定性原理比基於標準差的熵不確定性原理更強，因為 $\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}\exp \left(H_{x}+H_{p}-\log \left({\壓裂{e\,h}{2\,x_{0}\,p_{0}}}\right)\right)\geq {\frac {\hbar }{2}}~.$

換句話說，海森堡不確定性原理是量子熵不確定性原理的結果，但反之則不然。關於這些不平等的一些評論。首先， e 基數的選擇是物理學中的流行慣例。對數也可以以任何底數表示，只要它在不等式兩邊都一致。其次，回想一下使用的是香農熵，而不是量子馮諾依曼熵。最後，常態分佈使不等式飽和，並且它是唯一具有此屬性的分佈，因為它是具有固定變異數的分佈中的最大熵機率分佈（請參閱此處的證明）。

常態分佈的熵不確定性

測量設備將具有有限的分辨率，該分辨率是通過將其可能的輸出離散化到箱中而設置的，並具有位於玻恩規則給出的箱之一內的概率。我們將考慮最常見的實驗情況，其中箱的大小一致。令δx為空間解析度的度量。我們將第零個 bin 置於原點附近的中心，可能會有一些小的常數偏移c。位於寬度δx的第 j 個區間內的機率為 $\operatorname {P} [x_{j}]=\int _{(j-1/2)\delta xc}^{(j+1/2)\delta xc}|\psi (x)| ^{2}\,dx$

為了解釋這種離散化，我們可以將給定測量設備的波函數的香農熵定義為 $H_{x}=-\sum _{j=-\infty }^{\infty }\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}].$

根據上述定義，熵不確定性關係為 ${\displaystyle H_{x}+H_{p}>\ln \left({\frac {e}{2}}\right)-\ln \left({\frac {\delta x\delta p}{h }}\正確的）。$

這裡我們注意到 $δx δp / h$ 是配分函數計算中所使用的典型無窮小相空間體積。不平等也是嚴格且未飽和的。努力改善這一界限是一個活躍的研究領域。

常態分佈範例

Sinc 函數範例

與三個角動量分量的不確定性關係

對於總角動量的粒子 $j$ 以下不確定性關係成立 $\sigma _{J_{x}}^{2}+\sigma _{J_{y}}^{2}+\sigma _{J_{z}}^{2}\geq j,$ 在哪裡 $J_{l}$ 是角動量分量。該關係可以從 $\langle J_{x}^{2}+J_{y}^{2}+J_{z}^{2}\rangle =j(j+1),$ 和 $\langle J_{x}\rangle ^{2}+\langle J_{y}\rangle ^{2}+\langle J_{z}\rangle ^{2}\leq j.$ 此關係可加強為^[ 30 ]^[ 84 ] $\sigma _{J_{x}}^{2}+\sigma _{J_{y}}^{2}+F_{Q}[\varrho ,J_{z}]/4\geq j,$ 在哪裡 $F_{Q}[\varrho ,J_{z}]$ 是量子費希爾資訊。

歷史

1925 年，海森堡發表了Umdeutung（重新詮釋）論文，其中顯示量子理論的核心面向是非交換性：該理論暗示位置和動量測量的相對順序是重要的。他與馬克斯·玻恩和帕斯誇爾·喬丹合作，繼續發展矩陣力學，這將成為第一個現代量子力學公式。^[ 85 ]

1926年3月，海森堡在玻爾研究所工作時認知到非交換性蘊含著不確定性原理。 1927 年 2 月，他寫信給沃夫岡·泡利，提出了基本概念。^[ 86 ]

在 1927 年著名的論文“ Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”（“論量子理論運動學和力學的感知內容”）中，海森堡將此表達式建立為由任何位置測量引起的不可由任何位置測量引起的不可由任何位置測量引起的避免的動量擾動的最小量，^[ 2 ]但他沒有給出不確定性Δx和Δp的精確定義。相反，他對每種情況分別給出了一些合理的估計。他的論文用顯微鏡進行了分析，但玻爾證明這是不正確的。海森堡為該出版物添加了一個附錄。

在 1930 年的芝加哥演講中^[ 87 ]，他完善了他的原則：

\Delta x\,\Delta p\gtrsim h

( A1 )

後來的工作拓寬了這個概念。任何兩個不交換的變數都不能同時測量——一個變數知道越精確，另一個變數知道得就越不精確。海森堡寫道：

它可以用最簡單的形式表達如下：人們永遠不可能完全準確地知道決定最小粒子之一運動的兩個重要因素——它的位置和速度。不可能在同一時刻準確地確定粒子的位置、方向和速度。^[⁸⁸^]

Kennard ^[ 6 ]^[ 1 ]^:204於1927年首次證明了現代不等式：

\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}

( A2 )

其中 $ħ = ⁠ 小時 / 2π ⁠$ 、 $σ x$ 、 $σ p$ 是位置和動量的標準差。（海森堡僅證明了高斯態特殊情況的關係（ A2 ）。 ^[ 87 ]）1929年，羅伯遜將不等式推廣到所有可觀測量，1930年，薛定諤擴展了該形式，以允許算子的非零協方差；這個結果被稱為羅伯遜-薛丁格不等式。^[ 1 ]^：204

術語和翻譯

在海森堡 1927 年用德語撰寫的原始論文的主體部分中，海森堡使用了「Ungenauigkeit」一詞，^[ 2 ] 來描述基本理論原則。只是在尾註他才改用「Unsicherheit」這個字。後來他一直用「Unbestimmtheit」。然而，海森堡教科書《量子理論的物理原理》的英文版於1930年出版時，只使用了英文單字“uncertainty”，並成為英語中的術語。^[ 89 ]

海森堡顯微鏡

這個原理是相當違反直覺的，因此必須向量子理論的早期學生保證，違反該原理的簡單測量必然是行不通的。海森堡最初說明違反不確定性原則本質上不可能的一種方法是使用想像的顯微鏡的觀察者效應作為測量裝置。 ^[ 87 ]

他想像實驗者試圖透過向電子發射光子來測量電子的位置和動量。^[⁹⁰^]^：49–50

問題 1 – 如果光子的波長較短，因此動量較大，則可以準確測量位置。但光子沿著隨機方向散射，將大量且不確定的動量傳遞給電子。如果光子具有長波長和低動量，則碰撞不會對電子動量產生太大幹擾，但散射只會模糊地揭示其位置。
問題2 – 如果顯微鏡使用大孔徑，可以很好地解析電子的位置（參見瑞利準則）；但根據動量守恆原理，入射光子的橫向動量會影響電子的束線動量，因此電子的新動量解析不佳。如果使用小光圈，兩種解析度的精度則相反。

這些權衡的結合意味著，無論使用什麼光子波長和孔徑尺寸，測量位置和測量動量的不確定性的乘積都大於或等於下限，即（最多一個小的數值因子） ) 等於普朗克常數。^[ 91 ]海森堡並不關心將不確定性原理表述為精確極限，而是更喜歡將其用作啟發式定量陳述，糾正較小的數值因子，這使得量子力學的全新非交換性不可避免。

內在的量子不確定性

從歷史上看，不確定性原理一直與物理學中的相關效應（稱為觀察者效應）混淆^[ 92 ]^[ 66 ] ，觀察者效應指出，無法在不影響系統的情況下對某些系統進行測量，^[⁹³^]^[⁹⁴^]也就是說，無需更改系統中的某些內容。海森堡在量子層面上使用這種觀察者效應（見下文）作為量子不確定性的物理「解釋」。^[⁹⁵^]然而，從那時起，人們變得更加清楚，不確定性原理是所有類波系統的固有屬性，^[⁶⁹^]並且它在量子力學中的出現僅僅是由於所有量子物體的物質波性質。 ^[⁹⁶^]因此，不確定性原理實際上陳述了量子系統的基本屬性，而不是對當前技術觀測成功的陳述。^[⁹⁷^]

批評反應

事實上，量子力學的哥本哈根解釋和海森堡的不確定性原理最初被批評者視為孿生目標。根據量子力學的哥本哈根解釋，量子態並不描述任何基本現實，只是計算實驗結果的處方。沒有辦法從根本上說明系統的狀態是什麼，只能說明觀察的結果可能是什麼。

阿爾伯特愛因斯坦認為隨機性反映了我們對現實的某些基本屬性的無知，而尼爾斯玻爾則認為機率分佈是基本的且不可約的，並且取決於我們選擇執行哪些測量。愛因斯坦和玻爾對測不準原理爭論了很多年。

理想的超然觀察者

沃夫岡·泡利稱愛因斯坦對不確定性原理的根本反對是「超然觀察者的理想」（這句話翻譯自德語）：

「就像月亮有一個確定的位置一樣，」愛因斯坦去年冬天對我說，「無論我們是否看月亮，原子物體也必須如此，因為這些物體和宏觀物體之間不可能有明顯的區別。觀察不能創造像位置這樣的現實元素，在物理現實的完整描述中必須包含一些東西，它與觀察位置的可能性相對應，而在實際進行觀察之前就已經存在了。我希望我正確引用了愛因斯坦的話；憑記憶引用某人不同意的觀點總是很困難的。我將這種假設稱為超然觀察者的理想。
— 泡利寫給尼爾斯·玻爾的信，1955 年 2 月 15 日^[ 98 ]

愛因斯坦的狹縫

愛因斯坦挑戰不確定原理的第一個思想實驗如下：

考慮一個粒子穿過寬度為 $d$ 的狹縫。狹縫引入了大約 $⁠的動量不確定性$ $小時 / d ⁠$ 因為粒子穿過牆壁。但是讓我們透過測量壁的反衝力來確定粒子的動量。在此過程中，我們透過動量守恆找到任意精確度的粒子動量。

玻爾的回答是，牆壁也是量子力學的，為了精確測量反沖力 $Δ p$ ，在粒子通過之前必須知道牆壁的動量。這引入了壁位置的不確定性，因此狹縫的位置等於 $⁠$ $小時 / Δp ⁠$ ，如果壁的動量已知足以精確地測量後座力，那麼狹縫的位置就足夠不確定，無法進行位置測量。

理查德·費曼 (Richard Feynman)對通過多個狹縫衍射的粒子進行了類似的分析。^[ 99 ]

愛因斯坦的盒子

當愛因斯坦提出思想實驗（後來被稱為愛因斯坦盒子）時，玻爾也在場。愛因斯坦認為，“海森堡的不確定性方程式暗示時間的不確定性與能量的不確定性有關，兩者的乘積與普朗克常數有關。” ^[ 100 ]他說，考慮一個理想的盒子，裡面襯有鏡子，這樣它就可以無限地容納光線。在發條機構在選定的時刻打開理想的快門以允許單個光子逸出之前，可以對盒子進行稱重。愛因斯坦解釋說：“我們現在確切地知道光子離開盒子的時間。” ^[ 101 ]「現在，再次稱一下盒子的重量。質量的變化表明了發射光的能量。愛因斯坦說，透過這種方式，人們可以以任何所需的精度測量發射的能量和釋放的時間，這與不確定性原理。^[ 100 ]

玻爾花了一個不眠之夜思考這個論點，最後意識到它是有缺陷的。他指出，如果要對盒子進行稱重，例如通過彈簧和秤上的指針進行稱重，“由於盒子必須隨著其重量的變化而垂直移動，因此其垂直速度將存在不確定性，因此.. ....此外，由於愛因斯坦自己的重力對時間的影響理論，地球表面以上高度的不確定性將導致時鐘速率的不確定性”，^[ 102 ]。 “透過這一系列的不確定性，玻爾表明愛因斯坦的燈箱實驗無法同時精確測量光子的能量和其逃逸時間。” ^[¹⁰³^]

糾纏粒子的 EPR 悖論

1935 年，愛因斯坦、鮑里斯·波多爾斯基和內森·羅森發表了對空間分離糾纏粒子的分析（EPR 悖論）。^[ 104 ]根據EPR，人們可以測量其中一個糾纏粒子的位置和第二個粒子的動量，並根據這些測量結果推斷出兩個粒子的位置和動量，達到任意精度，這違反了不確定性原理。為了避免這種可能性，一個粒子的測量必須立即修改另一個粒子的機率分佈，這可能違反局部性原理。^[ 105 ]

1964 年，約翰·斯圖爾特·貝爾 (John Stewart Bell)表明，這一假設可以被證偽，因為它意味著不同實驗的機率之間存在一定的不平等。實驗結果證實了量子力學的預測，排除了EPR局部隱變數的基本假設。

波普爾的批評

科學哲學家卡爾·波普爾以邏輯學家和形上學實在論者的身份探討了不確定性問題。^[ 106 ]他不同意將不確定性關係應用於單一粒子而不是相同製備的粒子的集合，並將它們稱為「統計散射關係」。^[ 106 ]^[ 107 ]在這種統計解釋中，可以以任意精度進行特定測量，而不會使量子理論失效。

1934年，波普在《Naturwissenschaften》中發表了《Zur Kritik der Ungenauigkeitsrelationen》（“對不確定性關係的批判”），^[¹⁰⁸^]，同年又發表了《Logik der Forschung》（作者於1959年翻譯並更新為《科學發現的邏輯》^[¹⁰⁶^]）），概述了他對統計解釋的論點。 1982年，他進一步發展了他的量子理論和物理學分裂理論，寫道：

毫無疑問，[海森堡]公式是量子理論的可推導統計公式。但它們經常被那些量子理論家所誤解，他們說這些公式可以被解釋為確定了我們測量精度的一些上限。 [原文強調] ^[ 109 ]

波普爾提出了一項偽造不確定性關係的實驗，儘管他後來在與卡爾·弗里德里希·馮·魏茨澤克、海森堡和愛因斯坦討論後撤回了最初的版本；波普爾把他的論文寄給了愛因斯坦，這可能影響了 EPR 悖論的表述。^[ 110 ]^：720

自由意志

包括阿瑟·康普頓（Arthur Compton ） ^[ 111 ]和馬丁·海森堡（Martin Heisenberg） [ ^112 ]在內的一些科學家認為，不確定性原理，或者至少是量子力學的一般概率性質，可能是自由意志兩階段模型的證據。然而，一種批評是，除了量子力學作為化學基礎的基本作用之外，由於量子系統在室溫下的快速退相干時間，需要量子力學的重要生物機制是不可能的。 ^[¹¹³^]該理論的支持者通常說，這種退相干可以透過生物細胞中發現的篩選和無退相干子空間來克服。^[¹¹³^]

熱力學

有理由相信，違反不確定原理也強烈意味著違反熱力學第二定律。^[ 114 ]參見吉布斯悖論。

拒絕原則

不確定性原理將量子粒子（例如電子）與經典概念（位置和動量）聯繫起來。這假設量子粒子具有位置和動量。Edwin C. Kemble在 1937 年指出^[ 115 ]^{[需要澄清]}，這些性質無法透過實驗驗證，假設它們存在會引起許多矛盾；同樣，魯道夫·哈格指出，量子力學中的位置是相互作用的屬性，例如電子和探測器之間的相互作用，而不是內在屬性。^[ 116 ]^[ 117 ]從這個角度來看，不確定性原理並不是一個基本的量子屬性，而是一個「從我們祖先的語言中繼承下來的」概念，正如肯布爾所說。

應用領域

由於不確定性原理是量子力學中的一個基本結果，因此量子力學中的典型實驗通常會觀察到它的各個方面。所有形式的光譜學，包括粒子物理學，都使用這種關係將測量的能量線寬與量子態的壽命聯繫起來。然而，某些實驗可能會故意測試不確定性原理的特定形式，作為其主要研究計劃的一部分。例如，其中包括超導^[ 118 ]或量子光學^[ 119 ]系統中數相不確定性關係的測試。依賴不確定性原理進行操作的應用包括極低噪音技術，例如重力波干涉儀所需的技術。^[ 120 ]

參見

對應原理－尼爾斯·玻爾提出的物理原理
古德哈特定律 – 關於統計措施的格言 – 當嘗試使用統計措施來達到控制（指導）的目的時，其統計有效性就會崩潰
量子力學導論 —非數學導論
Küpfmüller 不確定原理 – Karl Küpfmüller 提出的電子工程概念
量子不確定性－在測量量子系統之前明顯缺乏確定的狀態
量子疊加 ——量子力學原理
量子穿隧 ——量子力學現象
物理學與超越 – 維爾納·海森堡 1969 年出版的書（海森堡的回憶）
更強的不確定性關係－海森堡原理的後期發展

量子力學
有關以下內容的系列文章的一部分
$i\hbar {\frac {d}{dt}}\|\Psi \rangle ={\hat {H}}\|\Psi \rangle$ 薛丁格方程
介紹詞彙表歷史
背景
基礎知識
實驗
配方
方程式
解釋貝葉斯一致的歷史哥本哈根德布羅意-博姆合奏隱變數當地的超決定論多世界客觀崩潰量子邏輯關係型交易性馮諾依曼-維格納
高級主題
科學家
v t e

在物理學中，隱變量理論是一種確定性物理模型，旨在透過引入額外的（可能無法訪問的）變數來解釋量子力學的機率性質。

假設測量前系統狀態的不確定性是量子力學數學公式的一部分；此外，不確定性的界限可以透過海森堡不確定性原理以定量形式表示。大多數隱變量理論都試圖避免這種不確定性，但可能以要求允許非局部交互作用為代價。一種著名的隱變量理論是德布羅意-玻姆理論。

1935 年，阿爾伯特·愛因斯坦、鮑里斯·波多爾斯基和內森·羅森在他們的EPR 論文中指出，量子糾纏可能表明量子力學是對現實的不完整描述。^[ 1 ]^[ 2 ] 約翰·斯圖爾特·貝爾於1964年在他的同名定理中證明，任何局部隱變量理論下粒子之間的相關性都必須遵守一定的約束。隨後，貝爾測試實驗證明了這些限制的廣泛違反，從而排除了此類理論。^[ 3 ]然而，貝爾定理並不排除非局域理論或超決定論的可能性；因此，貝爾測試不能證偽這些。

動機

宏觀物理學需要經典力學，能夠以可重複的高精度準確預測機械運動。量子現象需要量子力學，而量子力學只能準確預測統計平均值。如果量子態具有等待巧妙的新測量技術的隱藏變量，那麼後者（統計結果）可能可以轉換為前者的一種形式（經典機械運動）。^[ 4 ]

這樣的經典力學將消除量子理論中令人不安的特徵，例如不確定性原理。然而，更根本的是，具有隱藏變數的量子現象的成功模型意味著具有獨立於測量的內在值的量子實體。現有的量子力學斷言，只有在測量之後才能知道狀態屬性。正如N. David Mermin所說：

「這是一個基本的量子學說，一般來說，測量不會揭示被測量屬性的預先存在的值。相反，測量的結果是由測量本身的行為產生的…」^[ 5 ]

換句話說，雖然隱變量理論意味著內在的粒子屬性，但在量子力學中，電子甚至沒有明確的位置和速度可以被揭示。

歷史

“上帝不玩骰子”

1926 年 6 月，馬克斯·玻恩發表了一篇論文，^[ 6 ]，他在論文中第一個明確闡述了量子波函數的概率解釋，該解釋是歐文·薛定諤在當年早些時候提出的。玻恩對此論文的結論如下：

這裡就出現了決定論的整個問題。從我們的量子力學的角度來看，在任何個別情況下，沒有任何量可以因果地決定碰撞的結果。但從實驗來看，我們到目前為止還沒有理由相信原子的某些內部特性決定了碰撞的決定結果。我們是否應該希望以後能發現這些性質……並在個別情況下確定它們？或者我們應該相信理論和實驗的一致性——關於不可能為因果演化規定條件——是一種建立在不存在這些條件的基礎上的預先建立的和諧？我自己傾向於放棄原子世界的決定論。但這是一個哲學問題，僅靠物論論證並不能起到決定性作用。

玻恩對波函數的解釋受到了薛丁格的批評，薛丁格之前曾試圖用真實的物理術語來解釋它，但阿爾伯特·愛因斯坦的回應成為最早、最著名的量子力學不完整的斷言之一：

量子力學是非常值得尊敬的。但內心的聲音告訴我這畢竟不是真品。這個理論提供了很多東西，但它幾乎沒有讓我們更接近舊日支配者的秘密。無論如何，我確信他不是在玩骰子。^[ 7 ]^[ 8 ]

據報道，尼爾斯·玻爾（Niels Bohr）對愛因斯坦後來表達的這種觀點做出了回應，建議他「停止告訴上帝該做什麼」。^[ 9 ]

隱變量理論的早期嘗試

在發表著名的「上帝不擲骰子」評論後不久，愛因斯坦試圖對量子力學制定一個確定性的反提議，並於 1927 年 5 月 5 日在柏林科學院的一次會議上發表了一篇論文，題為“最佳薛定諤的Wellenmechanik” die Bewegung eines Systems vollständig oder nur im Sinne der Statistik？（「薛丁格的波動力學是完全決定係統的運動還是僅在統計意義上決定係統的運動？」）。^[ 10 ]^[ 11 ] 然而，當這篇論文準備在科學院期刊上發表時，愛因斯坦決定撤回它，可能是因為他發現，與他的意圖相反，他使用薛定諤場來引導局域粒子只允許他打算避免的那種非本地影響。^[ 12 ]

1927 年 10 月，在比利時舉行的第五屆索爾維大會上，當時所有主要的理論物理學家都出席了會議，路易斯·德布羅意提出了他自己的確定性隱變量理論版本，顯然沒有意識到愛因斯坦在今年早些時候的失敗嘗試。在他的理論中，每個粒子都有一個相關的、隱藏的“導波”，用於引導其在空間中的軌跡。該理論在大會上受到了批評，特別是沃夫岡·泡利的批評，德布羅意沒有充分回答這一點。此後不久，德布羅意就放棄了這個理論。

量子力學完整性聲明以及玻爾-愛因斯坦之爭

同樣在第五屆索爾維大會上，馬克斯·玻恩（Max Born）和沃納·海森堡（Werner Heisenberg）做了演講，總結了量子力學最近巨大的理論發展。在演講結束時，他們宣布：

[W]雖然我們考慮......電磁場的量子力學處理......尚未完成，但我們認為量子力學是一個封閉的理論，其基本物理和數學假設不再容易受到任何修改。 .. 關於「因果律的有效性」問題，我們有這樣的觀點：只要只考慮我們目前獲得的物理和量子力學經驗領域內的實驗，原則上非決定論的假設，這裡被視為基本原理，與經驗一致。^[ 13 ]

儘管沒有愛因斯坦在第五屆索爾維大會的技術會議上對玻恩和海森堡做出回應的記錄，但他確實在不同時期挑戰了量子力學的完整性。在博恩退休的紀念文章中，他討論了宏觀球在剛性障礙物之間彈性彈跳的量子表示。他認為，這種量子表示並不代表一個特定的球，而是「系統的時間集合」。因此，這種表述是正確的，但並不完整，因為它不能代表真實的個體宏觀情況。^[ 14 ]愛因斯坦認為量子力學是不完整的，「因為狀態函數一般來說甚至不能描述單一事件/系統」。^[ 15 ]

馮諾依曼的證明

約翰·馮·諾伊曼 (John von Neumann)在其 1932 年出版的《量子力學的數學基礎》一書中證明了量子力學中不可能存在「隱藏參數」。 1935 年，格蕾特·赫爾曼 (Grete Hermann)對馮·諾依曼證明的有效性提出了質疑，他發現了證明中的缺陷。關鍵問題涉及整體的平均值。馮·諾依曼假設不同可觀測量的期望值之間的關係對於「隱藏參數」的每個可能值都成立，而不僅僅是它們的統計平均值。^[ 16 ]^[ 17 ]然而，赫爾曼的工作幾乎沒有被注意到，直到 30 多年後被約翰·斯圖爾特·貝爾 (John Stewart Bell) 重新發現。^[ 18 ]^[ 19 ]

馮·諾依曼證明的有效性和確定性也受到漢斯·賴興巴赫的質疑，並且可能在阿爾伯特·愛因斯坦的談話中提出，但沒有發表。據報道，大約在 1938 年，在與助手彼得·伯格曼和瓦倫丁·巴格曼的一次談話中，愛因斯坦從書架上取下了馮·諾依曼的書，指出了赫爾曼和貝爾批評的相同假設，並詢問為什麼人們應該相信它。^[ 20 ]^[ 21 ] Simon Kochen和Ernst Specker早在¹⁹⁶¹年就拒絕了馮諾依曼的關鍵假設，但直到 1967 年才發表對其的^批評。

EPR悖論

愛因斯坦認為，量子力學不可能是物理現實的完整理論。他寫道，

考慮一個由兩個部分系統A和B組成的機械系統，它們僅在有限的時間內相互作用。給出它們相互作用之前的ψ函數 [即波函數]。然後薛定諤方程式將在相互作用發生後提供ψ函數。現在讓我們透過測量盡可能完整地確定部分系統A的物理狀態。然後，量子力學允許我們根據所做的測量來確定部分系統B的ψ函數，以及整個系統的ψ函數。然而，這種確定給出的結果取決於A的哪些物理量（可觀測量）已被測量（例如，坐標或動量）。由於相互作用後B只能有一種物理狀態，而不能合理地認為該狀態取決於我們對與B分離的系統A進行的特定測量，因此可以得出結論，ψ函數並未明確地與物理狀態協調。幾個ψ函數與系統B的相同物理狀態的協調再次表明ψ函數不能被解釋為單一系統物理狀態的（完整）描述。^[²³^]

愛因斯坦與鮑里斯·波多爾斯基和內森·羅森一起發表了一篇論文，提出了反對量子力學完整性的相關但獨特的論點。^[ 24 ]他們提出了一個思想實驗，涉及一對在後來被稱為糾纏態的粒子。愛因斯坦、波多爾斯基和羅森指出，在這種狀態下，如果測量到第一個粒子的位置，就可以預測測量到第二個粒子位置的結果。如果測量第一個粒子的動量，則可以預測測量第二個粒子動量的結果。他們認為，對第一個粒子採取的任何行動都不會立即影響另一個粒子，因為這將導致訊息傳輸速度超過光速，而根據相對論，這是不可能的。他們引用了後來被稱為「現實的 EPR 標準」的原則，假設：「如果在不以任何方式乾擾系統的情況下，我們可以確定地（即機率等於一）預測物理量的值，那麼存在與該量相對應的現實元素。由此，他們推斷第二個粒子在測量任一量之前必須具有確定的位置值和動量值。但量子力學認為這兩個可觀察量不相容，因此不會將兩者的同時值與任何系統關聯起來。因此，愛因斯坦、波多爾斯基和羅森得出結論，量子理論並沒有提供現實的完整描述。^[ 25 ]

玻爾對愛因斯坦-波多爾斯基-羅森挑戰的回答如下：

愛因斯坦、波多爾斯基和羅森的[論點]對於「不以任何方式乾擾系統」這一表述的含義含糊不清。 …… [E]即使在這個階段[即測量，例如，作為糾纏對一部分的粒子]，本質上存在對定義可能的預測類型的條件的影響的問題關於系統未來的行為。由於這些條件構成了「物理現實」一詞可以正確附加到的任何現象的描述的固有要素，因此我們看到上述作者的論證並不能證明他們的結論，即量子力學描述本質上是不完整的。 ” ^[ 26 ]

玻爾在這裡選擇將「物理現實」定義為僅限於可以透過任意選擇和明確指定的技術立即觀察到的現象，使用他自己對「現象」一詞的特殊定義。他於 1948 年寫道：

作為一種更合適的表達方式，人們可能會強烈主張限制現像一詞的使用，僅指在特定情況下獲得的觀察結果，包括對整個實驗的描述。^[ 27 ]^[ 28 ]

當然，這與 EPR 的現實標準相衝突。

貝爾定理

1964年，約翰·斯圖爾特·貝爾透過他著名的定理證明，如果存在局部隱變量，則可以進行涉及量子糾纏的某些實驗，其結果將滿足貝爾不等式。另一方面，如果量子糾纏產生的統計相關性無法用局部隱變數來解釋，則會違反貝爾不等式。關於隱變數理論的另一個不可行定理是科亨-斯佩克定理。

Alain Aspect和 Paul Kwiat等物理學家進行的實驗發現，這些不等式的違反程度高達 242 個標準差。^[ 29 ]這排除了局部隱變數理論，但不排除非局部隱變數理論。理論上，可能存在影響實驗結果有效性的實驗問題。

Gerard 't Hooft基於超決定論漏洞對貝爾定理的有效性提出了質疑，並提出了一些建構局部決定論模型的想法。^[ 30 ]^[ 31 ]

玻姆的隱變量理論

1952年，大衛·博姆提出隱變數理論。玻姆在不知不覺中重新發現（並擴展）了路易斯·德布羅意的導波理論於 1927 年提出（並放棄）的想法，因此該理論通常被稱為“德布羅意-玻姆理論」。假設貝爾定理的有效性，任何與量子力學一致的確定性隱變量理論都必須是非局域的，在物理上分離的實體之間維持瞬時或超光速關係（相關性）的存在。

玻姆提出了量子粒子（例如電子）和控制其運動的隱藏「導波」。因此，在這個理論中，電子顯然是粒子。當進行雙縫實驗時，電子穿過任一縫。此外，穿過的狹縫不是隨機的，而是受（隱藏的）導頻波控制，產生觀察到的波形。

在玻姆的解釋中，（非局域）量子勢構成了組織粒子的隱含（隱藏）秩序，它本身可能是另一個隱含秩序的結果：組織場的超隱含秩序。 ^[ 32 ]如今，玻姆的理論被認為是量子力學的多種解釋之一。有些人認為這是解釋量子現象的最簡單的理論。 ^[ 33 ]儘管如此，它是一個隱變數理論，而且必然如此。^[ 34 ]當今玻姆理論的主要參考文獻是他與巴茲爾‧海利 (Basil Hiley)合作出版的著作。^[ 35 ]

玻姆理論的一個可能的弱點是，有些人（包括愛因斯坦、泡利和海森堡）認為它看起來很做作。^[ 36 ]（事實上，玻姆認為這是他最初對理論的表述。^[ 37 ]）玻姆說，他認為他的理論作為物理理論是不可接受的，因為導波存在於抽象的多維構型空間中，而不是作為物理理論。^[ 37 ]

參見

在量子力學中，超決定論是貝爾定理的一個漏洞。透過假設所有被測量的系統都與對其進行哪些測量的選擇相關，該定理的假設不再滿足。因此，超決定論的隱變數理論可以滿足貝爾的局部因果關係概念，但仍違反貝爾定理導出的不等式。^[¹^]這使得建構再現量子力學預測的局部隱變數理論成為可能，為此提出了一些玩具模型。 ^[²^]^[³^]^[⁴^]除了確定性之外，超確定性模型也假設測量的狀態與測量設定之間的相關性。

概述

貝爾定理假設每個偵測器執行的測量可以彼此獨立地選擇，也可以獨立於決定測量結果的隱藏變數來選擇。這種關係通常被稱為測量獨立性或統計獨立性。在超決定論理論中，這種關係不成立。隱藏變數必然與測量設定相關。由於測量的選擇和隱藏變數是預先確定的，一個探測器的結果可以取決於另一個探測器進行的測量，而不需要資訊以比光速更快的速度傳播。統計獨立性的假設有時被稱為自由選擇或自由意志假設，因為它的否定意味著人類實驗學家不能自由選擇要執行的測量。

可以測試超決定論的受限版本，該版本假設隱藏變數與測量選擇之間的相關性在最近已經建立。^[ 5 ]不過，一般來說，超決定論從根本上來說是不可檢驗的，因為可以假設自大爆炸以來相關性就存在，從而使漏洞無法消除。^[ 6 ]

1980 年代，約翰‧史都華‧貝爾 (John Stewart Bell)在BBC訪談中討論了超決定論：^[ 7 ]^[ 8 ]

有一種方法可以擺脫超光速和遠距離幽靈行動的影響。但它涉及宇宙的絕對決定論，以及自由意志的完全缺失。假設世界是超級確定性的，不僅無生命的自然在幕後發條運行，而且我們的行為，包括我們相信我們可以自由選擇做一個實驗而不是另一個實驗，是絕對預先確定的，包括“當實驗當者決定進行一組測量而不是另一組測量時，困難就消失了。不需要比光更快的訊號來告訴粒子 A 對粒子 B 進行了什麼測量，因為宇宙，包括粒子 A，已經「知道」該測量及其結果將是什麼。

儘管他承認有漏洞，但他也認為這是難以置信的。即使所執行的測量是由確定性隨機數產生器選擇的，這些選擇也可以被假定為“對於當前的目的來說是有效自由的”，因為機器的選擇會被大量非常小的影響所改變。隱藏變數不太可能像隨機數產生器那樣對所有相同的小影響敏感。^[ 9 ]

諾貝爾物理學獎得主Gerard 't Hooft在 20 世紀 80 年代初期與 John Bell 討論了這個漏洞：

我提出了這個問題：假設愛麗絲和鮑伯的決定也必須被視為不是出於自由意志，而是由理論中的一切決定。約翰說，好吧，你知道，我必須排除這一點。如果可以的話，那我說的就不適用了。我說，愛麗絲和鮑伯做出的決定是有原因的。原因在於他們的過去，必須包含在圖片中」。^[ 10 ]

根據物理學家安東·蔡林格的說法，如果超決定論是正確的，它的一些含義將透過破壞可證偽性來質疑科學本身的價值：

我們總是隱含地假設實驗者的自由……這個基本假設對科學研究至關重要。如果這不是真的，那麼，我認為，在實驗中提出自然問題就毫無意義了，因為那時自然可以決定我們的問題是什麼，並且可以引導我們的問題，從而使我們得出錯誤的圖景自然的。^[ 11 ]

物理學家薩賓·霍森菲爾德（Sabine Hossenfelder）和蒂姆·帕爾默（Tim Palmer）認為，超決定論「是一種很有前途的方法，不僅可以解決測量問題，而且可以理解量子物理的明顯非定域性」。^[ 12 ]

霍華德·M·懷斯曼（Howard M. Wiseman）和埃里克·卡瓦爾坎蒂（Eric Cavalcanti）認為，任何假設的超決定論「都與普遍存在的外星精神控制的信念一樣合理且有吸引力」。^[ 13 ]

範例

^第^一個超確定性隱變數模型由^Carl^H. Brans於1988年^提出^。^[⁴^] Gerard 't Hooft將他的量子力學元胞自動機模型稱為超決定論^[¹⁴^]，儘管目前尚不清楚它是否滿足定義。

有些作者認為量子力學中的逆因果關係是超決定論的一個例子，而其他作者則將這兩種情況視為不同的情況。^[ 15 ]不存在區分它們的一致定義。

上帝擲骰子嗎？測不準原理和隱變數理論