悠日記: 觀察者效應（物理）

觀察者效應（物理）

其他用途，請參閱觀察者效應。

量子力學
有關以下內容的系列文章的一部分
$i\hbar {\frac {d}{dt}}\|\Psi \rangle ={\hat {H}}\|\Psi \rangle$ 薛丁格方程
介紹詞彙表歷史
背景
基礎知識
實驗
配方
方程式
解釋
高級主題
科學家
v t e

在物理學中，觀察者效應是指觀察行為對被觀察系統的干擾。^[ 1 ]^[ 2 ]這通常是使用儀器的結果，這些儀器必然會以某種方式改變其測量的狀態。一個常見的例子是檢查汽車輪胎的壓力，這會導致一些空氣逸出，從而改變觀察到的壓力大小。同樣，看到不發光的物體需要光線照射到物體上，使其反射光線。雖然觀察的影響通常可以忽略不計，但物體仍然會經歷變化（導致薛丁格的貓思想實驗）。這種效應可以在物理學的許多領域中發現，但通常可以透過使用不同的儀器或觀察技術將其降低到微不足道的程度。

雙縫實驗證明了量子力學中觀察者效應的一個顯著例子。物理學家發現，透過偵測器或儀器對量子現象的觀察可以改變該實驗的測量結果。儘管雙縫實驗中的「觀察者效應」是由電子探測器的存在引起的，但實驗結果被一些人解釋為表明意識可以直接影響現實。^[³^]然而，「觀察者」需要有意識並沒有得到科學研究的支持，並且被指出是一種誤解，根源在於對量子波函數 $ψ$ 和量子測量過程的理解不足。^[⁴^]^[⁵^]^[⁶^]

粒子物理學

電子在與光子相互作用時被檢測到；這種相互作用將不可避免地改變該電子的速度和動量。其他不太直接的測量方法也可能影響電子。也必須清楚地區分數量的測量值和測量過程所產生的值。特別是，動量的測量在短時間內是不可重複的。Niels Bohr (1928)提出的相關量的公式（為簡單起見，為一維）由下式給出： $|v'_{x}-v_{x}|\Delta p_{x}\approx \hbar /\Delta t,$ 在哪裡

$Δ p x$ 是動量測量值的不確定度，
$Δ t$ 是測量持續時間，
$v x$ 是測量前粒子的速度，
$v' x$ 為測量後粒子的速度，
$ħ$ 是簡化的普朗克常數。

測得的電子動量與 v x 相關， $而測量$ 後的電子動量與 $v' x$ 相關。這是最好的情況。^[ 7 ]

電子產品

在電子設備中，電流表和電壓表通常與電路串聯或併聯，因此它們的存在會透過向電路提供額外的真實或複雜負載來影響它們所測量的電流或電壓，從而改變傳輸電路本身的和行為。即使是更被動的設備，例如電流鉗，無需與電線物理接觸即可測量電線電流，也會影響通過被測電路的電流，因為電感是相互的。

熱力學

在熱力學中，標準的玻璃水銀溫度計必須吸收或釋放一些熱能來記錄溫度，從而改變所測量的物體的溫度。

量子力學

量子力學的一些解釋認為量子現象的觀察者扮演核心角色。 ^[ 8 ]量子力學觀察者與觀察者效應問題息息相關，其中測量必然需要與被測量的物理對象相互作用，透過相互作用影響其屬性。術語「可觀察」已經獲得了技術意義，表示代表測量的厄米算符。 ^[ 9 ]^：55

參見

觀察者（狹義相對論）

觀測者效應（Observer effect），是指「觀測」這種行為對被觀測對象造成一定影響的效應。

在量子力學實驗中，如果要測算一個電子所處的速度，就要用兩個光子隔一段時間去撞擊這個電子，但第一個光子就已經把這個電子撞飛了，便改變了電子的原有速度，我們便無法測出真正準確的速度（不確定原理）^[1]。時間流逝的快慢也會受到觀測者的影響，用很高的頻率去觀測粒子的衰變，反而使得粒子長時間不衰變^[2]。

在狹義相對論中，觀察者是一個參考系，從中測量一組物體或事件。通常這是一個慣性參考系或“慣性觀察者”。較不常見的是，觀察者可以是任意非慣性參考系，例如可稱為「加速觀察者」的 Rindler 參考系。

狹義相對論的用法與「觀察者」的普通英語意義有很大不同。參考系本質上是非局部構造，涵蓋所有空間和時間或其重要部分；因此，說觀察者（在狹義相對論意義上）有一個位置是沒有意義的。此外，慣性觀察者不能稍後加速，加速觀察者也不能停止加速。

物理學家使用術語「觀察者」作為特定參考系的簡寫，從中測量一組物體或事件。說到狹義相對論中的觀察者，並不是專門假設正在經歷事件的個人，而是要評估物體和事件的特定數學背景。無論慣性參考系內是否有知覺存在，狹義相對論的效應都會發生。

歷史

愛因斯坦在其 1905 年關於狹義相對論的原創論文以及對該主題的早期流行闡述中頻繁使用“觀察者”（Beobachter ）一詞。 ^[ 1 ]然而，他在白話意義上使用了這個術語，例如指「火車車廂窗口的人」或「以火車為參考體的觀察者」或「內部配備了設備」。這裡，參考體或座標系（覆蓋事件發生的時空區域的米尺和時鐘的物理排列）與觀察者（透過觀察（字面意思是看到）將時空座標分配給遠離自己的事件的實驗者）區分開來。

觀察者和觀察者的「裝置」（如座標系、測量工具等）之間的這種區別被許多後來的作者放棄了，今天，「觀察者」一詞通常用來暗示觀察者的相關座標系（通常假設為由垂直於類時向量（幀場，請參見 Doran ^[ 2 ]）。愛因斯坦提到“以火車為參考體的觀察者”或“位於坐標係原點的觀察者”，這群現代作家說，例如，“觀察者由坐標系表示空間和時間的四個變量” ^[ 3 ]或「 S 座標系中的觀察者發現某個事件A發生在他的座標係原點」。^[ 4 ]然而，在這一點上並沒有達成一致，許多作者仍然傾向於區分觀察者（作為與運動狀態相關的概念）和坐標系的更抽象的一般數學概念（可以是，但不一定是，與運動有關）。這種方法更強調對觀察者開放的多種描述選擇。然後用觀察參考系來辨識觀察者，而不是用座標系、測量設備和運動狀態的組合來辨識。 ^[ 5 ]^[ 6 ]^[ 7 ]^[ 8 ]^[ 9 ]

也有人建議，「觀察員」一詞已經過時，應該用觀察員小組（或觀察員家庭）取代，其中每個觀察員在其附近進行觀察，延遲可以忽略不計，並與其他觀察員合作。同步時鐘，所有團隊成員將其各種結果發送回資料收集器進行綜合。^[ 10 ]

「觀察者」作為相對座標的一種形式

相對方向是許多人類語言中的概念。在英語中，對物體的空間位置的描述可以使用諸如“左”和“右”之類的術語，這些術語相對於說話者或相對於特定物體或視角（例如“在你的左邊，當你面對著物體時」）。前門」）。

這種描述的主觀程度相當微妙。請參閱奧茲瑪問題來了解這一點。

語言中相對方向的一些客觀例子是航海術語“船頭”、 “船尾” 、“左舷”和“右舷”。這些是相對的、自我中心型的空間術語，但它們不涉及自我：即使船上沒有人，船也有船頭、船尾、左舷和右舷。

涉及「觀察者」的狹義相對論在某種程度上闡明了類似的客觀相對方向。「觀察者」是一種視角，因為它是評估其他慣性參考系中的事件的上下文，但它不是單一特定人所擁有的那種視角：它不是本地化的，並且不與特定的對象相關聯。

在其他科學學科中的用途

觀察者一詞在其他科學領域也具有特殊意義，例如量子力學和資訊理論。例如，參見薛丁格的貓和麥克斯韋的惡魔。

在廣義相對論中，「觀察者」一詞更常見地指進行被動局部測量的人（或機器），這種用法更接近該詞的普通英語含義。在量子力學中，「觀察」與量子測量同義，「觀察者」與測量儀器同義，「可觀察」與可測量的東西同義。物理學中的這種用法衝突有時會造成混亂。

參見

^惠勒的延遲選擇實驗描述了約翰·阿奇博爾德·惠勒 (John Archibald Wheeler)提出的^一系列量子物理學思想實驗，其中最著名的出現在 1978 年和 1984 年^。說明了量子理論的中心點：

將光子從進入點到最後飛行瞬間的整個旅行過程歸因於有形性是錯誤的。^[ 2 ]^：184

這些實驗彌補了傳統雙縫實驗中的一個漏洞，即量子行為取決於實驗安排。該漏洞被稱為「陰謀」模型，其中光以某種方式「感知」實驗裝置，調整其行為以適應粒子或波的行為。透過在光子「飛行」後改變裝置，漏洞就被堵住了。延遲選擇的宇宙版本使用數十億年前發射的光子；結果沒有變化。^[ 3 ] 延遲選擇的概念已經產生了許多具有啟發意義的實驗。^[ 4 ] 延遲選擇概念的新版本使用量子效應來控制“選擇”，從而導致了量子延遲選擇實驗。

概念

惠勒的延遲選擇實驗表明，沒有符合相對論的粒子傳播模型可以解釋量子理論。^[ 2 ]^: 184與雙縫實驗一樣，惠勒的概念在源和偵測器之間有兩條等效路徑。與雙縫的單向版本一樣，該實驗有兩種版本：一種旨在檢測波干涉，另一種旨在檢測粒子。惠勒方法中的新成分是這兩個實驗之間的延遲選擇。測量波干涉或粒子路徑的決定被延遲到檢測之前。目標是確保在做出實驗選擇之前，任何行進的粒子或波都會通過量子系統中兩條不同路徑的區域。^[ 5 ]^： 967

宇宙干涉儀

這張影像中心顯示的雙類星體是一顆距離地球近 90 億光年的恆星，由於重力透鏡作用，它產生了兩幅影像。 ^[ 6 ]

本節沒有引用任何來源。請透過添加對可靠來源的引用來幫助改進本節。無源材料可能會受到質疑並被刪除。 （2018 年 10 月）（了解如何以及何時刪除此訊息）

本文可能會讓讀者感到困惑或不清楚。請幫忙澄清這篇文章。討論頁上可能會對此進行討論。 （2018 年 10 月）（了解如何以及何時刪除此訊息）

惠勒的宇宙干涉儀使用一個遙遠的類星體，有兩條路徑到達地球上的設備，一條是直接的，另一條是透過重力透鏡。之後^[ 2 ]

為了避免破壞正常的因果觀念，一些理論家^[誰？ ]表明，關於是否安裝了第二個分束器的信息可以以某種方式從實驗設備的端點傳輸回剛剛進入該實驗設備的光子，從而允許它做出正確的“決定。”因此惠勒提出了他的實驗的宇宙版本。在那個思想實驗中，他問如果距離地球數百萬或數十億光年的類星體或其他星系將其光線傳遞到充當重力透鏡的中間星系或星系團周圍，會發生什麼事。精確射向地球的光子會遇到中間的大質量星系附近的空間扭曲。到那時，它必須「決定」是否以粒子的形式繞透鏡星系單向傳播，或以波的形式雙向傳播。當光子到達地球的天文台時，會發生什麼事？由於重力透鏡效應，天文台中的望遠鏡可以看到同一個類星體的兩幅影像，一幅在透鏡星系的左側，一幅在透鏡星系的右側。如果光子以粒子的形式傳播並進入瞄準左側類星體圖像的望遠鏡的鏡筒，那麼它一定決定以粒子的形式傳播數百萬年，至少一些實驗者是這麼說的。那台望遠鏡指向了錯誤的方向，無法從另一張類星體影像中拾取任何東西。如果光子作為粒子傳播並以相反的方式傳播，那麼它只會被指向正確「類星體」的望遠鏡接收到。因此，數百萬年前，光子決定以粒子的形式行進，並隨機選擇了另一條路徑。但實驗者現在決定嘗試其他方法。他們將兩個望遠鏡的輸出引導到分束器，如圖所示，並發現一個輸出非常明亮（表明正干涉），而另一個輸出基本上為零，表明傳入的波函數對已自抵消。

惠勒隨後扮演了魔鬼的擁護者，並表示，也許要獲得的實驗結果意味著，在天文學家插入分束器的那一刻，數百萬年前離開類星體的光子決定以波的形式傳播，而當天作家決定再次拉出分束器時，這項決定會透過時間傳遞回數百萬年加幾分鐘前的光子，因此光子回溯性地決定以粒子的形式傳播。

實現惠勒基本思想的幾種方法已被納入實際實驗中，它們支持惠勒預期的結論^{[需要引用]} ——在檢測到光子之前在實驗裝置的出口處所做的事情將決定它是否表現出干涉現像或不。

雙縫版本

惠勒的雙縫裝置。^[ 7 ]

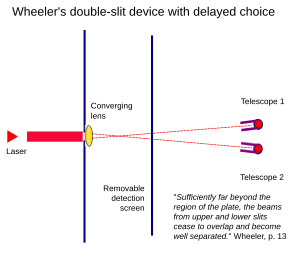
第二種實驗類似普通的雙縫實驗。實驗的示意圖顯示，雙縫遠端的透鏡使來自每個狹縫的路徑在距離該透鏡相當近的地方彼此交叉後稍微發散。結果是每個光子的兩個波函數將在雙縫相當短的距離內疊加，並且如果在波函數疊加的區域內提供檢測螢幕，則將看到干涉圖案。沒有任何方法可以確定任何給定的光子是從雙縫之一到達的。然而，如果移除偵測螢幕，每條路徑上的波函數將疊加在越來越低振幅的區域上，並且它們的組合機率值將遠小於每條路徑中心處的未增強機率值。當望遠鏡瞄準截取兩條路徑的中心時，光子出現在其中一條路徑中的機率接近 50%。當望遠鏡 1 偵測到光子時，研究人員可能會將光子與從下部狹縫中出現的波函數連結起來。當望遠鏡 2 中偵測到一個光子時，研究人員可能會將該光子與從上部狹縫中出現的波函數連結起來。支持這種實驗結果解釋的解釋是，一個光子從其中一個狹縫中出現，這就是問題的終點。光子必須從雷射開始，穿過其中一個狹縫，並通過一條直線路徑到達相應的望遠鏡。

惠勒不接受的逆因果解釋說，隨著偵測螢幕的到位，幹擾一定會顯現出來。為了使乾涉顯現出來，光波必須從兩個狹縫中的每一個出現。因此，進入雙縫光闌的單一光子必須「決定」它需要穿過兩個縫才能在偵測螢幕上乾擾自身。為了不干涉，進入雙縫光闌的單個光子必須「決定」僅通過一個縫，因為這將使它出現在適當的單望遠鏡的相機上。

在這個思想實驗中，望遠鏡總是存在的，但是實驗可以從存在檢測屏幕開始，然後在光子離開雙縫光闌後立即將其移除，或者實驗可以從不存在檢測屏幕開始，然後將其移除。一些理論家認為，在實驗過程中插入或移除螢幕可以迫使光子在之前以波的形式穿過雙縫時，追溯性地決定以粒子的形式穿過雙縫，反之亦然。惠勒不接受這種解釋。

雙縫實驗與其他六個理想化實驗（顯微鏡、分裂光束、傾斜齒、輻射方向圖、單光子偏振和成對光子偏振）一樣，要求在互補觀察模式之間進行選擇。在每個實驗中，我們都找到了一種方法，可以將要尋找的現象類型的選擇延遲到現象發展的最後階段，這取決於我們隨後採用的檢測設備類型。這種延遲對實驗預測沒有影響。在這一點上，我們發現的一切都在玻爾那句孤獨而意味深長的句子中得到了預示：「…就透過明確的實驗安排獲得的可觀察到的效果而言，無論我們建造或處理儀器的計劃如何，它……都沒有什麼區別。 ”是預先確定的，還是我們是否願意推遲完成計劃，直到粒子已經從一個儀器到另一個儀器的途中。” ^[ 8 ]

波希米亞解釋

在玻姆對量子力學的解釋中，粒子服從經典力學，只不過它的運動是在其量子勢的額外影響下發生的。^[ 9 ]^[ 10 ]^[ 11 ]^{: 279}光子或電子具有明確的軌跡，並且穿過兩個狹縫中的一個或另一個，而不是同時穿過兩個狹縫，就像經典粒子的情況一樣。當將其作為波檢測的實驗配置改變為在到達時間T _2檢測粒子的實驗配置時，過去被確定並保持在T ₁時刻之前的狀態。在T ₁處，當實驗設定改變時，玻姆的量子勢會根據需要而變化，並且粒子在新的量子勢下經典地移動，直到T ₂當其被檢測為粒子時。因此，波姆力學恢復了對世界及其過去的傳統看法。過去是客觀的歷史，無法透過延遲的選擇來改變。量子勢包含有關定義系統的邊界條件的信息，因此實驗設置的任何變化都會反映在決定粒子動力學的量子勢的變化中。^[¹¹^]^{: 6.7.1}然而，量子勢是非局域的，它的任何變化都是瞬時的，這與相對論不一致。^[¹²^]^：121

實驗細節

約翰·惠勒(John Wheeler) 對延遲選擇量子可能性的最初討論出現在一篇題為“沒有法律的法律”的文章中，該文章發表在他和沃伊切赫·休伯特·祖雷克(Wojciech Hubert Zurek) 編輯的《量子理論與測量》一書中，第 182-213 頁。他在演講中重申了阿爾伯特·愛因斯坦（Albert Einstein）和尼爾斯·玻爾（Niels Bohr）之間的爭論，前者想要一個可理解的現實，後者認為愛因斯坦的現實概念過於狹隘。惠勒指出，愛因斯坦和玻爾探索了下面將要討論的實驗室實驗的結果，其中光可以從半鍍銀和全鍍銀鏡子矩形陣列的一個角到達另一個角，然後可以不僅顯示為沿著單一路徑繞了周界一半然後退出，而且還顯示為繞著周界雙向行駛，然後“做出了選擇”，是從一個端口退出還是從一個端口退出另一個。這個結果不僅適用於光束，也適用於單光子。惠勒評論道：

愛因斯坦和玻爾討論的干涉儀形式的實驗理論上可以用來研究光子是否有時沿著單一路徑出發，總是遵循兩條路徑但有時只使用一條路徑，或者是否會出現其他東西。然而，說「我們將在實驗的隨機運行期間，在光子到達那裡之前插入第二個半銀鏡」比找出一種方法來製造如此快速的結果更容易。光速太快，機械設備無法完成這項工作，至少在實驗室範圍內是如此。解決這個問題需要很多聰明才智。

在發表了幾個支持實驗後，雅克等人。聲稱他們的實驗完全遵循惠勒提出的原始方案。^[ 13 ]^[ 14 ]他們的複雜實驗是基於Mach-Zehnder干涉儀，涉及觸發鑽石N-V色心光子產生器、偏振和充當可切換分束器的電光調製器。在封閉配置中進行測量會出現幹擾，而在開放配置中進行測量則可以確定粒子的路徑，因此不可能產生幹擾。

實驗室中的干涉儀

惠勒版本的干涉儀實驗直到最近才在實驗室中進行，因為在光子進入第一個分束器和到達該位置之間的短暫時間間隔內插入或移除第二個分束器存在實際困難為第二分束器提供。該實驗的實現是透過插入較長的光纜來延長兩條路徑的長度來完成的。這樣做使得通過設備所涉及的時間間隔更長。一條路徑上的高速可切換設備由高壓開關、普克爾斯盒和格蘭湯普森棱鏡組成，可以將該路徑從其普通目的地轉向，從而使該路徑實際上進入死胡同。當繞行運作時，任何探測器都無法通過該路徑到達任何探測器，因此不會產生幹擾。關閉後，路徑恢復其正常作用模式並穿過第二個分束器，從而再次出現幹擾。這種佈置實際上並沒有插入和移除第二分束器，但是它確實使得可以從出現干涉的狀態切換到不出現干涉的狀態，並且在進入第一光束的光之間的間隔中進行切換-分束器和從第二分束器射出的光。如果光子「決定」以波或粒子的形式進入第一個分束器，那麼它們一定被指示撤銷該決定並以其他形式通過系統，並且它們一定是在沒有任何物理過程的情況下這樣做的被中繼到進入的光子或第一個分束器，因為即使在光速下，這種傳輸也太慢。惠勒對物理結果的解釋是，在兩個實驗的一種配置中，在一個或其他探測器處以50% 的機率接收到進入光子的波函數的單一副本，而在另一種配置下，接收到進入光子的波函數的兩個副本波函數通過不同的路徑傳播，到達兩個探測器，彼此異相，因此表現出乾涉。在一個偵測器中，波函數將彼此同相，結果將是光子有 100% 的機率出現在該偵測器中。在另一個偵測器中，波函數將出現 180° 異相，將完全相互抵消，且其相關光子出現在該偵測器中的機率為 0%。^[ 15 ]

宇宙中的干涉儀

惠勒所設想的宇宙實驗可以描述為類似於干涉儀實驗或類似雙縫實驗。重要的是，透過第三種裝置，即充當重力透鏡的巨大恆星物體，來自源頭的光子可以通過兩條路徑到達。根據波函數對之間的相位差如何排列，可以相應地觀察到不同種類的干涉現象。是否合併傳入的波函數以及如何合併傳入的波函數可以由實驗者控制。實驗裝置沒有像實驗室干涉儀實驗那樣在波函數中引入相位差，因此儘管光源附近沒有雙縫裝置，但宇宙實驗更接近雙縫實驗。然而，惠勒計劃在實驗中使用分束器合併傳入的波函數。^[ 16 ]

進行這個實驗的主要困難在於，實驗者無法控製或不知道每個光子何時開始向地球旅行，實驗者不知道遙遠類星體之間兩條路徑中每條路徑的長度。因此，一個波函數的兩個副本很可能在不同時間到達。及時匹配它們以便它們能夠交互需要在第一個到達時使用某種延遲裝置。在完成該任務之前，有必要找到計算時間延遲的方法。

同步來自這個宇宙實驗裝置兩端的輸入的一個建議在於類星體的特徵以及識別某些訊號特徵的相同事件的可能性。惠勒用作推測基礎的來自雙類星體的資訊大約相隔 14 個月到達地球。^[ 17 ]要找到一種方法將光量子保持在某種循環中一年多並不容易。

實驗室與宇宙中的雙縫

透過在公共偵測螢幕上註冊投影望遠鏡影像來替換分光鏡。

惠勒版本的雙縫實驗的安排使得從兩個縫中出現的相同光子可以透過兩種方式檢測到。第一種方法讓兩條路徑匯聚在一起，讓波函數的兩個副本重疊，並顯示干涉。第二種方式遠離光子源，到達波函數的兩個副本之間的距離太大而無法顯示干涉效應的位置。實驗室的技術問題是如何在適當的位置插入探測器螢幕以觀察干涉效應，或移除該螢幕以露出光子探測器，該探測器只能接收來自狹縫所在空間的狹窄區域的光子。完成該任務的一種方法是使用最近開發的電動可切換鏡子，並透過打開或關閉鏡子來簡單地改變來自狹縫的兩條路徑的方向。截至 2014 年初，尚未宣布此類實驗。

惠勒所描述的宇宙實驗還有其他問題，但在所涉及的光子可能「決定」是波還是粒子很久之後，將波函數副本引導到一個地方或另一個地方根本不需要很高的速度。人們大約有十億年的時間來完成這項工作。

干涉儀實驗的宇宙版本可以適應作為宇宙雙縫裝置的功能，如圖所示。^[ 18 ]^：66

目前感興趣的實驗

Walborn等人進行的第一個真正的實驗遵循了惠勒的雙縫裝置的意圖，以進行檢測方法的最終決定。 ^[ 19 ]

研究人員使用最初為SETI研究設計的電波望遠鏡，解釋了進行星際惠勒實驗的實際困難。^[ 20 ]

量子延遲選擇實驗

新版本的延遲選擇實驗不是機械地激活延遲，而是設計了兩條由量子效應控制的路徑。然後，整個實驗創建兩個結果（粒子行為或波行為）的疊加。事實證明，這條實驗線在最初構思時非常難以實施。儘管如此，多年來它已被證明非常有價值，因為它引導研究人員提供「單量子波粒二象性的日益複雜的演示」。^[ 21 ]^[ 22 ]正如一位實驗者所解釋的那樣，“波和粒子行為可以同時共存。” ^[ 23 ]

曼寧等人最近的一項實驗。用氦原子證實了標準量子力學的標準預測。^[ 24 ]

提出了宏觀量子延遲選擇實驗：兩個奈米碳管的相干耦合可以透過放大的單聲子事件來控制。^[ 25 ]

結論

馬，澤林格等人。總結了惠勒提議中產生的實驗結果。他們說：

我們的工作證明並證實了兩個糾纏光子之間的相關性是否揭示了welcher-weg [“which-way”] 資訊或一個（系統）光子的干涉圖案取決於對另一個（環境）光子的測量選擇，甚至當兩側可類空分離的事件全部類空分離時。事實上，可以確定波或粒子特徵是否在測量很久之後（甚至是與空間分離）才顯現出來，這一事實告訴我們，我們不應該有任何幼稚的現實圖像來解釋量子現象。對一個光子的特定單獨觀察中發生的情況的任何解釋都必須考慮到由兩個光子組成的完整量子態的整個實驗裝置，並且只有在記錄了所有有關互補變量的信息後才有意義。我們的結果表明，系統光子要么表現為波，要么表現為粒子的觀點需要比光速更快的通訊。因為這與狹義相對論有強烈的張力，我們認為這種觀點應該完全放棄。^[ 26 ]

歷史

約翰·惠勒，1985

延遲選擇實驗的概念^始於量子物理學中的一系列思想實驗，^由^惠勒^於1978 年首次^提出^。測量光子的「類似」（具有頻率或振幅）屬性，但不能同時測量兩者。測量哪種特性取決於實驗者是否使用旨在觀察粒子或觀察波的設備。^[²⁹^]當這一說法被非常嚴格地應用時，人們可能會爭辯說，通過確定探測器類型，可以迫使光子僅表現為粒子或波。光子的偵測通常是一個破壞性過程（有關非破壞性測量，請參閱量子非破壞測量）。例如，光子可以被檢測為被光電倍增管中的電子吸收的結果，光電倍增管接受其能量，然後用於觸發級聯事件，從該設備產生“咔噠”聲。在雙縫實驗中，光子在螢幕上顯示為空間和時間上高度局部化的點。光子在螢幕上的累積表明光子是否必須以波的形式穿過狹縫，或者是否可以以粒子的形式傳播。如果累積導致波的典型乾涉圖案，則稱光子以波的形式傳播（有關顯示累積的動畫，請參閱雙縫實驗§來自單個粒子的干涉）。然而，如果關閉其中一個狹縫，或者在狹縫前面放置兩個正交偏振器（使穿過不同狹縫的光子可區分），則不會出現干涉圖案，並且可以將累積現象解釋為光子作為粒子行進。

參見

量子退相干是量子相干性的損失。研究量子退相干是為了了解量子系統如何轉換成可以用經典力學解釋的系統。從試圖擴展對量子力學的理解開始，該理論已向多個方向發展，實驗研究已經證實了一些關鍵問題。量子計算依賴量子相干性，是此概念的主要實際應用之一。

概念

在量子力學中，物理系統由稱為量子態的數學表示來描述。透過將玻恩規則應用於描述該系統的量子態來計算系統實驗結果的機率。量子態不是純態，就是混合態；純態也稱為波函數。為量子系統分配純態意味著該系統上某些測量結果的確定性，即存在一種測量，其中一種可能的結果將以機率 1 發生。時間統一演化。因此，純量子態保持純淨。然而，如果系統沒有完全隔離，例如在測量過程中，相干性就會與環境共享，並且似乎會隨著時間的推移而消失，這一過程稱為量子退相干或環境退相干。量子相干性並沒有消失，而是與環境中更多的自由度混合在一起，類似於經典力學中能量實際上在環境中產生熱量時因摩擦而損失的方式。

退相干可以被視為從系統到環境的資訊遺失（通常建模為熱浴），^[ 1 ]因為每個系統都與其周圍的能量狀態鬆散耦合。孤立地看，系統的動態是非單一的（儘管組合系統加環境以單一的方式演化）。^[ 2 ]因此，系統的動態本身是不可逆的。與任何耦合一樣，系統和環境之間會產生糾纏。這些具有與周圍環境共享量子資訊或將其傳輸到周圍環境的效果。

歷史與解釋

與量子力學解釋的關係

量子力學的解釋是試圖解釋量子物理學的數學理論如何與經驗的現實相對應。^[ 3 ]退相干計算可以用量子力學的任何解釋來完成，因為這些計算是量子理論標準數學工具的應用。然而，退相干主題在整個歷史中一直與解釋問題密切相關。^[ 4 ]^[ 5 ]

退相干已被用來理解量子力學中波函數崩潰的可能性。退相干不會產生實際的波函數塌縮。它僅提供了明顯的波函數塌縮的框架，因為量子系統的組件與同一環境中的其他量子系統糾纏在一起。也就是說，波函數的分量與相干系統解耦並從其直接周圍環境獲取相位。全域或通用波函數的完全疊加仍然存在（並且在全局層面上保持相干），但其最終命運仍然是一個解釋問題。

關於測量問題，退相干為系統向混合狀態的轉變提供了解釋，這些狀態似乎與觀察者感知的狀態相對應。此外，觀察結果表明，這種混合物在測量情況下看起來像一個適當的量子係綜，因為測量導致「實現」「係綜」中精確的一種狀態。

維爾納·海森堡和尼爾斯·玻爾的哲學觀點經常被歸類為“哥本哈根解釋”，儘管他們在重要觀點上存在重大分歧。^[ 6 ]^[ 7 ] 1955年，海森堡提出系統與其周圍環境的相互作用將消除量子乾涉效應。然而，海森堡沒有詳細說明這是如何發生的，也沒有明確說明糾纏在這個過程中的重要性。^[ 7 ]^[ 8 ]

概念的起源

內維爾·莫特 (Nevill Mott ) 在 1929 年解決標誌性莫特問題被認為是第一個量子退相干工作。^[ 9 ]它被第一個現代理論治療所引用。^[ 10 ]

儘管他沒有使用這個術語，但量子退相干的概念是由美國物理學家戴維·博姆（David Bohm）於1951年首次提出的，^[ 11 ]^[ 12 ]他稱之為「測量過程中乾擾的破壞”。玻姆後來使用退相干來處理量子理論的德布羅意-玻姆解釋中的測量過程。^[ 13 ]

1970 年，德國物理學家H. Dieter Zeh進一步強調了退相干的重要性，^[ 14 ]，自 20 世紀 80 年代以來，它一直是一個活躍的研究主題。^[ 15 ]退相干已經發展成為一個完整的框架，但正如退相干理論的創始人在他們的開創性論文中所承認的那樣，它是否解決了測量問題存在爭議。 ^[ 16 ]

退相干作為一個真正的主題的研究始於 1970 年 H. Dieter Zeh 的論文「論量子理論中測量的解釋」。^[ 4 ]^[ 14 ] Zeh 將波函數視為一個物理實體，而不是一種計算裝置或統計資訊概要（哥本哈根型解釋的典型特徵），他提出波函數應該統一演化，符合薛丁格方程，任何時候。 Zeh 最初並不知道Hugh Everett III的早期工作，^[ 17 ]該工作也提出了統一演化的通用波函數；在透過布萊斯·德威特（ Bryce DeWitt）的一篇文章了解到埃弗雷特的「相對狀態解釋」後，他修改了論文以引用埃弗雷特。^[ 4 ]（德威特將埃弗雷特的提議稱為多世界解釋，這個名字眾所周知。）對於 Zeh 來說，如何解釋量子力學的問題至關重要，並且沿著以下思路進行解釋：埃弗里特的是最自然的。部分原因是物理學家對解釋問題普遍不感興趣，Zeh 的工作一直相對被忽視，直到 20 世紀 80 年代初，當時Wojciech Zurek ^[ 18 ]^[ 19 ]的兩篇論文為這個主題注入了活力。與 Zeh 的出版物不同，Zurek 的文章對解釋相當不可知，而是關注密度矩陣動力學的具體問題。祖雷克對退相干的興趣源於玻爾在回答愛因斯坦-波多爾斯基-羅森悖論時進一步分析了雙縫實驗，這是他與比爾·伍特斯共同開展的工作，^[ 20 ]，此後他認為退相干帶來了一種和解。^[ 4 ]^[ 21 ]

退相干並不聲稱為某些實際的波函數崩潰提供了一種機制。相反，它為波函數塌縮的出現提出了一個合理的框架。系統的量子性質只是與環境糾纏在一起，因此波函數的總疊加仍然存在，但存在（至少對於所有實際目的）超出了測量領域。^[ 22 ]^[ 23 ]根據定義，合併但不可測量的波函數仍然存在的說法無法透過實驗證明。需要退相干來理解為什麼量子系統在與其環境相互作用後開始遵守經典機率規則（由於在將玻恩機率規則應用於系統時幹擾項被抑制）。

安東尼·萊格特（Anthony Leggett）對退相干理論解決測量問題的充分性提出了批評。^[ 24 ]^[ 25 ]

機制

為了研究退相干如何運作，下面提出了一個「直覺」模型。此模型需要熟悉量子理論基礎。在可視化經典相空間和希爾伯特空間之間進行了類比。狄拉克符號的更嚴格推導顯示了退相干如何破壞幹擾效應和系統的「量子性質」。接下來，提出密度矩陣方法以供透視。

透過拉比振盪進行量子態疊加和退相干測量

相空間圖

N粒子系統可以用波函數在非相對論量子力學中表示 $\psi (x_{1},x_{2},\dots ,x_{N})$ ，其中每個x _i是 3 維空間中的一個點。這與經典相空間有類比。經典相空間包含 6 N維的實值函數（每個粒子貢獻 3 個空間座標和 3 個動量）。另一方面，在這種情況下，「量子」相空間涉及 3 N維空間上的複值函數。位置和動量由不交換的算子表示，並且 $\psi$ 存在於希爾伯特空間的數學結構。然而，除了這些差異之外，粗略的類比也是成立的。

不同的先前孤立的、不相互作用的系統佔據不同的相空間。或者我們可以說它們在聯合系統的相空間中佔據不同的低維子空間。系統相空間的有效維數是存在的自由度數，在非相對論模型中，它是系統自由粒子數的 6 倍。對於宏觀系統來說，這將是一個非常大的維度。然而，當兩個系統（環境是一個系統）開始互動時，它們相關的狀態向量不再受限於子空間。相反，組合狀態向量隨時間演化一條通過「較大體積」的路徑，其維度是兩個子空間維度的總和。兩個向量相互幹擾的程度是它們在相空間中彼此「接近」程度的度量（正式來說，它們的重疊或希爾伯特空間相乘）。當系統耦合到外部環境時，聯合狀態向量的維數以及可用的「體積」大大增加。每個環境自由度都會貢獻一個額外的維度。

原始系統的波函數可以透過多種不同的方式擴展為量子疊加中的元素總和。每個展開對應於波矢量到基底上的投影。基礎可以隨意選擇。選擇一種擴展，其中所得到的基本元素以特定於元素的方式與環境相互作用，這些元素將以壓倒性的概率通過它們沿著自己的獨立路徑的自然單一時間演化而快速地彼此分離。經過很短的互動後，幾乎沒有進一步幹擾的機會。該過程實際上是不可逆的。在與環境耦合產生的擴展相空間中，不同的元素實際上彼此「丟失」。在相空間中，這種解耦是透過維格納準機率分佈來監控的。據說原始元素已經散焦。環境有效地選擇了原始狀態向量的那些彼此退相干（或失去相位相干性）的擴展或分解。這稱為“環境引起的超級選擇”，或“選擇性選擇” 。^[ 26 ]系統的退相干元件不再像雙縫實驗那樣表現出彼此之間的量子乾涉。任何透過環境相互作用而相互退相干的元素都被認為與環境發生了量子糾纏。反之則不然：並非所有糾纏態都會彼此退相干。

任何測量裝置或儀器都充當環境，因為在測量鏈的某個階段，它必須足夠大才能被人類讀取。它必須擁有大量隱藏的自由度。實際上，相互作用可以被認為是量子測量。由於相互作用，系統和測量裝置的波函數彼此糾纏。當系統波函數的不同部分以不同方式與量測設備糾纏時，就會發生退相干。為了使糾纏系統狀態的兩個選定元素干涉，原始系統和兩個元素裝置中的測量都必須在標量積意義上顯著重疊。如果測量裝置具有許多自由度，則這種情況發生的可能性 很小。

因此，該系統表現為不同元素的經典統計係綜，而不是它們的單一相干量子疊加。從每個集合成員的測量設備的角度來看，系統似乎已經不可逆轉地崩潰到具有相對於該元素的測量屬性的精確值的狀態。這提供了一種解釋，說明玻恩法則係數如何根據構成量子測量問題解決方案的測量假設有效地充當機率。

狄拉克記數法

使用狄拉克記號，讓系統初始處於狀態

|\psi \rangle =\sum _{i}|i\rangle \langle i|\psi \rangle ,

哪裡的 $|i\rangle$ s形成一個einselected基礎（環境誘導選擇的特徵基礎^[ 26 ]），並讓環境最初處於狀態 $|\epsilon \rangle$ 。系統和環境組合的向量基底由兩個子系統的基底向量的張量積組成。因此，在兩個子系統之間進行任何交互作用之前，聯合狀態可以寫為

|{\text{before}}\rangle =\sum _{i}|i\rangle |\epsilon \rangle \langle i|\psi \rangle ,

在哪裡 $|i\rangle |\epsilon \rangle$ 是張量積的簡寫 $|i\rangle \otimes |\epsilon \rangle$ 。系統與其環境互動的方式有兩個極端：(1) 系統失去其獨特的身份並與環境融合（例如，寒冷、黑暗的空腔中的光子轉換為空腔壁內的分子激發）， (2)即使環境受到干擾，系統也完全不受干擾（例如理想化的無幹擾測量）。一般來說，交互作用是我們研究的這兩個極端的混合。

系統被環境吸收

如果環境吸收了系統，則整個系統基礎的每個元素都會與環境相互作用，這使得

|i\rangle |\epsilon \rangle

演變成

|\epsilon _{i}\rangle ,

所以

|{\text{before}}\rangle

演變成

|{\text{after}}\rangle =\sum _{i}|\epsilon _{i}\rangle \langle i|\psi \rangle .

時間演化的么正性要求總狀態基底保持正交，即基底向量的標量或內積必須消失，因為 $\langle i|j\rangle =\delta _{ij}$ :

\langle \epsilon _{i}|\epsilon _{j}\rangle =\delta _{ij}.

環境狀態的這種正交性是選擇所需的定義特徵。^[ 26 ]

系統不受環境幹擾

在理想化測量中，系統會幹擾環境，但本身不受環境幹擾。在這種情況下，基礎的每個元素都與環境相互作用，使得

|i\rangle |\epsilon \rangle

演變為產品

|i,\epsilon _{i}\rangle =|i\rangle |\epsilon _{i}\rangle ,

所以

|{\text{before}}\rangle

演變成

|{\text{after}}\rangle =\sum _{i}|i,\epsilon _{i}\rangle \langle i|\psi \rangle .

在這種情況下，統一性要求

\langle i,\epsilon _{i}|j,\epsilon _{j}\rangle =\langle i|j\rangle \langle \epsilon _{i}|\epsilon _{j}\rangle =\delta _{ij}\langle \epsilon _{i}|\epsilon _{j}\rangle =\delta _{ij}\langle \epsilon _{i}|\epsilon _{i}\rangle =\delta _{ij},

在哪裡 $\langle \epsilon _{i}|\epsilon _{i}\rangle =1$ 被使用了。此外，由於環境中存在大量隱藏的自由度，退相干要求：

\langle \epsilon _{i}|\epsilon _{j}\rangle \approx \delta _{ij}.

和以前一樣，這是退相干成為選擇的決定性特徵。^[ 26 ]隨著受影響的環境自由度數的增加，近似變得更加精確。

請注意，如果系統基礎 $|i\rangle$ 不是一個單獨選擇的基礎，那麼最後一個條件是微不足道的，因為受干擾的環境不是 $我$ ，我們就有了微不足道的受干擾環境基礎 $|\epsilon _{j}\rangle =|\epsilon '\rangle$ 。這對應於系統基礎相對於環境定義的測量可觀測值而言是退化的。對於複雜的環境交互作用（典型的宏觀交互作用），很難定義非選擇性基礎。

幹擾損失以及從量子機率到經典機率的轉變

退相干的實用性在於其應用於環境交互作用前後的機率分析，特別是退相干發生後量子乾涉項的消失。如果我們問觀察到系統從 $\psi$ 到 $\phi$ 前 $\psi$ 已與其環境相互作用，則應用玻恩機率規則表明轉移機率是兩個狀態標量積的平方模：

\operatorname {prob} _{\text{before}}(\psi \to \phi )=\left|\langle \psi |\phi \rangle \right|^{2}=\left|\sum _{i}\psi _{i}^{*}\phi _{i}\right|^{2}=\sum _{i}|\psi _{i}^{*}\phi _{i}|^{2}+\sum _{ij;i\neq j}\psi _{i}^{*}\psi _{j}\phi _{j}^{*}\phi _{i},

在哪裡 $\psi _{i}=\langle i|\psi \rangle$ , $\psi _{i}^{*}=\langle \psi |i\rangle$ ，和 $\phi _{i}=\langle i|\phi \rangle$ ETC。

上述轉移機率的展開包含下列項： $i\neq j$ ;這些可以被認為代表不同基本元素或量子替代品之間的干擾。這是純粹的量子效應，代表了量子替代方案的機率的非可加性。

計算觀測到系統發生量子躍遷的機率 $\psi$ 到 $\phi$ 後 $\psi$ 與其環境相互作用，那麼應用玻恩機率規則表明我們必須對所有相關的可能狀態求和 $|\epsilon _{i}\rangle$ 模數平方之前的環境：

\operatorname {prob} _{\text{after}}(\psi \to \phi )=\sum _{j}\,\left|\langle {\text{after}}\right|\phi ,\epsilon _{j}\rangle |^{2}=\sum _{j}\,\left|\sum _{i}\psi _{i}^{*}\langle i,\epsilon _{i}|\phi ,\epsilon _{j}\rangle \right|^{2}=\sum _{j}\left|\sum _{i}\psi _{i}^{*}\phi _{i}\langle \epsilon _{i}|\epsilon _{j}\rangle \right|^{2}.

當我們應用退相干/選區條件時，內部求和消失 $\langle \epsilon _{i}|\epsilon _{j}\rangle \approx \delta _{ij}$ ，公式簡化為

\operatorname {prob} _{\text{after}}(\psi \to \phi )\approx \sum _{j}|\psi _{j}^{*}\phi _{j}|^{2}=\sum _{i}|\psi _{i}^{*}\phi _{i}|^{2}.

如果我們將其與環境引入退相干之前導出的公式進行比較，我們可以看到退相干的效果是移動了求和符號 $\textstyle \sum _{i}$ 從模數符號的內部到外部。因此，所有交叉或量子乾涉項

\sum _{ij;i\neq j}\psi _{i}^{*}\psi _{j}\phi _{j}^{*}\phi _{i}

已從轉移機率計算中消失。退相干已不可逆地將量子行為（加性機率振幅）轉換為經典行為（加性機率）。^[ 26 ]^[ 27 ]^[ 28 ] 然而，Ballentine ^[ 29 ]表明，退相干對減少干擾的顯著影響不一定對量子系統向經典極限的轉變具有重要意義。

就密度矩陣而言，幹擾效應的損失對應於「環境追蹤」密度矩陣的對角化。^[ 26 ]

密度矩陣法

退相干對密度矩陣的影響本質上是聯合系統密度矩陣的部分跡的非對角線元素的衰減或快速消失，即組合系統的密度矩陣相對於任何環境基礎的跡。退相干不可逆地將「平均」或「環境追蹤」^[²⁶^]密度矩陣從純狀態轉換為減少的混合物；正是這一點導致了波函數塌縮的出現。同樣，這被稱為“環境引起的超級選擇”或“選擇”。^[²⁶^]採取部分痕跡的優點是該程序與所選的環境基礎無關。

最初，組合系統的密度矩陣可以表示為

\rho =|{\text{before}}\rangle \langle {\text{before}}|=|\psi \rangle \langle \psi |\otimes |\epsilon \rangle \langle \epsilon |,

在哪裡 $|\epsilon \rangle$ 是環境的狀態。那麼，如果轉變發生在系統與環境之間發生任何交互作用之前，則環境子系統沒有部分並且可以被追蹤出來，從而為系統留下約簡密度矩陣：

\rho _{\text{sys}}=\operatorname {Tr} _{\textrm {env}}(\rho )=|\psi \rangle \langle \psi |\langle \epsilon |\epsilon \rangle =|\psi \rangle \langle \psi |.

現在轉移機率將給出為

\operatorname {prob} _{\text{before}}(\psi \to \phi )=\langle \phi |\rho _{\text{sys}}|\phi \rangle =\langle \phi |\psi \rangle \langle \psi |\phi \rangle ={\big |}\langle \psi |\phi \rangle {\big |}^{2}=\sum _{i}|\psi _{i}^{*}\phi _{i}|^{2}+\sum _{ij;i\neq j}\psi _{i}^{*}\psi _{j}\phi _{j}^{*}\phi _{i},

在哪裡 $\psi _{i}=\langle i|\psi \rangle$ , $\psi _{i}^{*}=\langle \psi |i\rangle$ ，和 $\phi _{i}=\langle i|\phi \rangle$ ETC。

現在是系統與環境互動後發生轉換的情況。組合的密度矩陣將是

\rho =|{\text{after}}\rangle \langle {\text{after}}|=\sum _{i,j}\psi _{i}\psi _{j}^{*}|i,\epsilon _{i}\rangle \langle j,\epsilon _{j}|=\sum _{i,j}\psi _{i}\psi _{j}^{*}|i\rangle \langle j|\otimes |\epsilon _{i}\rangle \langle \epsilon _{j}|.

為了獲得系統的約化密度矩陣，我們追蹤環境並採用退相干/選別條件，發現非對角項消失（Erich Joos 和 HD Zeh 在 1985 年獲得的結果）：^[ 30 ]

\rho _{\text{sys}}=\operatorname {Tr} _{\text{env}}{\Big (}\sum _{i,j}\psi _{i}\psi _{j}^{*}|i\rangle \langle j|\otimes |\epsilon _{i}\rangle \langle \epsilon _{j}|{\Big )}=\sum _{i,j}\psi _{i}\psi _{j}^{*}|i\rangle \langle j|\langle \epsilon _{j}|\epsilon _{i}\rangle =\sum _{i,j}\psi _{i}\psi _{j}^{*}|i\rangle \langle j|\delta _{ij}=\sum _{i}|\psi _{i}|^{2}|i\rangle \langle i|.

類似地，過渡後的最終約簡密度矩陣將是

\sum _{j}|\phi _{j}|^{2}|j\rangle \langle j|.

轉移機率將給出為

\operatorname {prob} _{\text{after}}(\psi \to \phi )=\sum _{i,j}|\psi _{i}|^{2}|\phi _{j}|^{2}\langle j|i\rangle \langle i|j\rangle =\sum _{i}|\psi _{i}^{*}\phi _{i}|^{2},

沒有乾擾項的貢獻

\sum _{ij;i\neq j}\psi _{i}^{*}\psi _{j}\phi _{j}^{*}\phi _{i}.

密度矩陣方法與波姆方法結合，產生了簡化軌跡方法，同時考慮了系統簡化密度矩陣和環境的影響。^[ 31 ]

運算符和表示

考慮一個系統S和環境（浴）B，它們是封閉的並且可以用量子力學來處理。讓 ${\mathcal {H}}_{S}$ 和 ${\mathcal {H}}_{B}$ 分別是系統的希爾伯特空間和浴的希爾伯特空間。那麼組合系統的哈密頓量為

{\hat {H}}={\hat {H}}_{S}\otimes {\hat {I}}_{B}+{\hat {I}}_{S}\otimes {\hat {H}}_{B}+{\hat {H}}_{I},

在哪裡 ${\hat {H}}_{S},{\hat {H}}_{B}$ 分別是系統哈密頓量和浴哈密頓量， ${\hat {H}}_{I}$ 是系統和浴之間的相互作用哈密頓量，並且 ${\hat {I}}_{S},{\hat {I}}_{B}$ 分別是系統和巴斯希爾伯特空間上的恆等算子。此封閉系統的密度算子的時間演化是酉的，因此由下式給出

\rho _{SB}(t)={\hat {U}}(t)\rho _{SB}(0){\hat {U}}^{\dagger }(t),

其中酉算符是 ${\hat {U}}=e^{-i{\hat {H}}t/\hbar }$ 。如果系統和浴最初沒有糾纏在一起，那麼我們可以寫 $\rho _{SB}=\rho _{S}\otimes \rho _{B}$ 。因此，系統的演化就變成了

\rho _{SB}(t)={\hat {U}}(t)[\rho _{S}(0)\otimes \rho _{B}(0)]{\hat {U}}^{\dagger }(t).

系統-浴相互作用哈密頓量可以寫成一般形式：

{\hat {H}}_{I}=\sum _{i}{\hat {S}}_{i}\otimes {\hat {B}}_{i},

在哪裡 ${\hat {S}}_{i}\otimes {\hat {B}}_{i}$ 是作用於組合系統 - 巴斯希爾伯特空間的算子，並且 ${\hat {S}}_{i},{\hat {B}}_{i}$ 是分別作用於系統和浴缸的操作員。系統和浴的這種耦合是系統中單獨退相干的原因。為了看到這一點，對浴進行部分追蹤以單獨給出系統的描述：

\rho _{S}(t)=\operatorname {Tr} _{B}{\big [}{\hat {U}}(t)[\rho _{S}(0)\otimes \rho _{B}(0)]{\hat {U}}^{\dagger }(t){\big ]}.

$\rho _{S}(t)$ 稱為約簡密度矩陣，僅給出有關係統的資訊。如果浴是根據其正交基 ket 的集合來寫的，也就是說，如果它最初已被對角化，則 $\textstyle \rho _{B}(0)=\sum _{j}a_{j}|j\rangle \langle j|$ 。計算相對於該（計算）基礎的部分跡給出

\rho _{S}(t)=\sum _{l}{\hat {A}}_{l}\rho _{S}(0){\hat {A}}_{l}^{\dagger },

在哪裡 ${\hat {A}}_{l},{\hat {A}}_{l}^{\dagger }$ 被定義為Kraus 運算子並表示為（索引 $我$ 結合指數 $k$ 和 $j$ ）：

{\hat {A}}_{l}={\sqrt {a_{j}}}\langle k|{\hat {U}}|j\rangle .

這稱為運算符和表示法(OSR)。 Kraus 算子的條件可以透過以下事實來獲得： $\operatorname {Tr} [\rho _{S}(t)]=1$ ;這然後給出

\sum _{l}{\hat {A}}_{l}^{\dagger }{\hat {A}}_{l}={\hat {I}}_{S}.

此限制決定了 OSR 中是否會發生退相干。特別是，當總和中存在不只一項時 $\rho _{S}(t)$ ，那麼系統的動力學將是非單一的，因此會發生退相干。

半群方法

主方程式給出了對量子系統中退相干存在性的更普遍的考慮，它決定了系統的密度矩陣如何隨時間演化（另請參見Belavkin^]³⁴^[^]³³^[^]³²^[方程式薛丁格圖，其中考慮了狀態的演化（由其密度矩陣表示）。主方程式是

\rho '_{S}(t)={\frac {-i}{\hbar }}{\big [}{\tilde {H}}_{S},\rho _{S}(t){\big ]}+L_{D}{\big [}\rho _{S}(t){\big ]},

在哪裡 ${\tilde {H}}_{S}=H_{S}+\Delta$ 是系統哈密頓量 $H_{S}$ 連同（可能的）單一捐款 $\Delta$ 從浴缸出來，以及 $L_{D}$ 是Lindblad 退相干術語。^[ 2 ] Lindblad 退相干項表示為

L_{D}{\big [}\rho _{S}(t){\big ]}={\frac {1}{2}}\sum _{\alpha ,\beta =1}^{M}b_{\alpha \beta }{\Big (}{\big [}\mathbf {F} _{\alpha },\rho _{S}(t)\mathbf {F} _{\beta }^{\dagger }{\big ]}+{\big [}\mathbf {F} _{\alpha }\rho _{S}(t),\mathbf {F} _{\beta }^{\dagger }{\big ]}{\Big )}.

這 $\{\mathbf {F} _{\alpha }\}_{\alpha =1}^{M}$ 是作用於系統希爾伯特空間的有界算子的M維空間的基算子 ${\mathcal {H}}_{S}$ 和是誤差產生器。^[ 35 ]矩陣元素 $b_{\alpha \beta }$ 表示正半定埃爾米特矩陣的元素；它們表徵了退相干過程，因此被稱為雜訊參數。^[ 35 ]半群方法特別好，因為它區分了酉過程和退相干（非酉）過程，而 OSR 則不然。特別地，非酉動力學表示為 $L_{D}$ ，而狀態的酉動力學則由通常的海森堡換向器表示。請注意，當 $L_{D}{\big [}\rho _{S}(t){\big ]}=0$ ，系統的動態演化是廬正的。主方程式所描述的系統密度矩陣的演化條件為：^[ 2 ]

系統密度矩陣的演化由單一參數半群決定
進化是「完全正向的」（即機率被保留）
系統和浴密度矩陣原本是解耦的

非單一建模範例

退相干可以建模為系統與其環境耦合的非單一過程（儘管組合的系統加環境以單一方式演化）。 ^[ 2 ]因此，單獨處理系統的動力學是非單一的，因此，由作用於系統希爾伯特空間的不可逆變換來表示 ${\mathcal {H}}$ 。由於系統的動力學是由不可逆的表示來表示的，因此量子系統中存在的任何資訊都可能會遺失到環境或熱浴中。或者，由系統與環境的耦合引起的量子資訊的衰減稱為退相干。^[ 1 ]因此，退相干是量子系統的資訊透過系統與其環境（形成封閉系統）的相互作用而改變的過程，從而在系統和熱浴（環境）之間產生糾纏。因此，由於系統以某種未知的方式與其環境糾纏在一起，因此如果不參考環境（即不描述環境的狀態），則無法對系統本身進行描述。

旋轉退相干

考慮一個對稱耦合到浴槽的N個量子位元系統。假設這個由N 個量子位元組成的系統圍繞 $|{\uparrow }\rangle \langle {\uparrow }|,|{\downarrow }\rangle \langle {\downarrow }|$ ${\big (}|0\rangle \langle 0|,|1\rangle \langle 1|{\big )}$ 本徵態 ${\hat {J_{z}}}$ 。那麼在這樣的旋轉下，隨機相 $\phi$ 將在本徵態之間創建 $|0\rangle$ , $|1\rangle$ 的 ${\hat {J_{z}}}$ 。因此這些基礎量子位元 $|0\rangle$ 和 $|1\rangle$ 將以以下方式轉變：

|0\rangle \to |0\rangle ,\quad |1\rangle \to e^{i\phi }|1\rangle .

此變換由旋轉運算子執行

R_{z}(\phi )={\begin{pmatrix}1&0\\0&e^{i\phi }\end{pmatrix}}.

由於該空間中的任何量子位元都可以用基礎量子位元來表示，因此所有此類量子位元都將在該旋轉下進行變換。考慮 $j$ 純狀態下的第 3 個量子位 $\vert \psi _{j}\rangle \langle \psi _{j}\vert$ 在哪裡 $|\psi _{j}\rangle =a|0\rangle +b|1\rangle$ 。在應用旋轉之前，該狀態為：

\rho _{j,{\text{init}}}={\begin{pmatrix}|a|^{2}&ab^{\ast }\\a^{\ast }b&|b|^{2}\end{pmatrix}}

。

此狀態將退相干，因為它不是用（取決於）移相因子「編碼」的 $e^{i\phi }$ 。這可以透過檢查隨機相上的平均密度矩陣來看出 $\phi$ :

\rho _{j}=\mathbb {E} [R_{z}(\phi )\vert \psi _{j}\rangle \langle \psi _{j}\vert R_{z}^{\dagger }(\phi )]=\int \limits _{-\infty }^{\infty }R_{z}(\phi )|\psi _{j}\rangle \langle \psi _{j}|R_{z}^{\dagger }(\phi )\;P({\text{d}}\phi )

,

在哪裡 $P(\cdot )$ 是隨機相位的機率度量， $\phi$ 。儘管並非完全必要，但為了簡單起見，讓我們假設這是由高斯分佈給出的，即 $P({\text{d}}\phi )={\frac {1}{{\sqrt {2\pi }}\sigma }}e^{-{\frac {1}{2}}({\frac {\phi }{\sigma }})^{2}}\,{\text{d}}\phi$ ，在哪裡 $\sigma$ 表示隨機相位的擴展。那麼依照上面計算的密度矩陣是

\rho _{j}={\begin{pmatrix}|a|^{2}&ab^{\ast }\,e^{-{\frac {1}{2}}\sigma ^{2}}\\a^{\ast }b\,e^{-{\frac {1}{2}}\sigma ^{2}}&|b|^{2}\end{pmatrix}}

。

觀察到非對角線元素（相干項）隨著隨機相位的擴展而衰減， $\sigma$ ，隨著時間的推移而增加（這是一個現實的期望）。因此，隨著時間的推移，系統每個量子位元的密度矩陣變得難以區分。這意味著沒有測量可以區分量子位元，從而在各種量子位元狀態之間產生退相干。特別是，這種相移過程導致量子位元崩潰到其中一種純態 $\{\vert 0\rangle \langle 0\vert ,\vert 1\rangle \langle 1\vert \}$ 。這就是為什麼這種類型的退相干過程被稱為集體相移，因為N量子位元系統的所有量子位元之間的相互相位都被破壞了。

去極化

去極化是量子系統上的一種非統一變換，它將純態映射到混合態。這是一個非酉過程，因為任何逆轉該過程的變換都會將狀態映射到各自的希爾伯特空間之外，從而不保留正性（即原始機率映射到負機率，這是不允許的）。這種變換的二維情況包括將布洛赫球表面上的純態映射到布洛赫球內的混合態。這將使布洛赫球體收縮一定的量，而相反的過程將使布洛赫球體膨脹，這是不可能發生的。

耗散

耗散是一種退相干過程，透過這個過程，量子態的數量由於與浴的糾纏而改變。一個例子是一個量子系統，它可以透過相互作用哈密頓量與浴交換能量。如果系統不處於基態且浴的溫度低於系統的溫度，則係統將向浴釋放能量，因此系統哈密頓量的較高能量本徵態將退相干到基態冷卻後，因此都不會退化。由於狀態不再退化，它們是不可區分的，因此這個過程是不可逆的（非統一的）。

時間尺度

對於宏觀物體來說，退相干代表了一個極其快速的過程，因為它們與許多微觀物體相互作用，在自然環境中具有大量的自由度。如果我們想要理解為什麼我們傾向於觀察不到日常宏觀物體中的量子行為，以及為什麼我們確實看到經典場是從大量物質的物質和輻射之間相互作用的特性中出現的，那麼這個過程是必要的。密度矩陣的非對角分量有效消失所需的時間稱為退相干時間。對於日常的宏觀過程來說，它通常非常短。^[ 26 ]^[ 27 ]^[ 28 ]退相干時間的現代獨立於基礎的定義依賴於初始狀態和時間相關狀態之間保真度的短時行為^[ 36 ]，或者等效地，純度的衰減。^[ 37 ]

數學細節

暫時假設所討論的系統由正在研究的子系統A和「環境」組成 $\epsilon$ ，總希爾伯特空間是希爾伯特空間的張量積 ${\mathcal {H}}_{A}$ 描述A和希爾伯特空間 ${\mathcal {H}}_{\epsilon }$ 描述 $\epsilon$ ，那是，

{\mathcal {H}}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{\epsilon }.

在A和A 的情況下，這是一個相當好的近似值 $\epsilon$ 是相對獨立的（例如，A的部分與A的部分混合） $\epsilon$ 或相反）。關鍵是，與環境的相互作用對於所有實際目的都是不可避免的（例如，即使真空中的單個受激原子也會發射光子，然後光子就會消失）。假設這種相互作用是透過作用於的單一變換 U來描述的 ${\mathcal {H}}$ 。假設環境的初始狀態為 $|{\text{in}}\rangle$ ， A的初始狀態是疊加態

c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle ,

在哪裡 $|\psi _{1}\rangle$ 和 $|\psi _{2}\rangle$ 是正交的，而且最初沒有糾纏。另外，選擇正交基 $\{|e_{i}\rangle \}_{i}$ 為了 ${\mathcal {H}}_{A}$ 。（這可能是「連續索引基礎」或連續索引和離散索引的混合，在這種情況下，我們必須使用操縱的希爾伯特空間，並且要更加小心正交規範的含義，但這對於說明目的來說是一個無關緊要的細節.）然後，我們可以擴展

U{\big (}|\psi _{1}\rangle \otimes |{\text{in}}\rangle {\big )}

和

U{\big (}|\psi _{2}\rangle \otimes |{\text{in}}\rangle {\big )}

獨特地作為

\sum _{i}|e_{i}\rangle \otimes |f_{1i}\rangle

和

\sum _{i}|e_{i}\rangle \otimes |f_{2i}\rangle

分別。需要認識到的一件事是，環境包含大量的自由度，其中許多自由度始終相互作用。這使得下面的假設在某種程度上是合理的，這在一些簡單的玩具模型中可以證明是正確的。假設存在一個基礎 ${\mathcal {H}}_{\epsilon }$ 這樣 $|f_{1i}\rangle$ 和 $|f_{1j}\rangle$ 如果i ≠ j則都近似正交，且對於 $|f_{2i}\rangle$ 和 $|f_{2j}\rangle$ 也為了 $|f_{1i}\rangle$ 和 $|f_{2j}\rangle$ 對於任何i和j（退相干屬性）。

在位置基礎上，這通常被證明是正確的（作為合理的猜想），因為A如何與環境互動通常關鍵取決於A中物件的位置。然後，如果我們對環境進行部分跟踪，我們會發現密度狀態^{[需要澄清]}大約可以描述為

\sum _{i}{\big (}\langle f_{1i}|f_{1i}\rangle +\langle f_{2i}|f_{2i}\rangle {\big )}|e_{i}\rangle \langle e_{i}|,

也就是說，我們有一個對角混合狀態，沒有相長或相消的干擾，並且「機率」按照經典方式相加。U ( t )（酉算符作為時間的函數）顯示退相干性質所需的時間稱為退相干時間。

實驗觀察

定量測量

退相干率取決於多種因素，包括溫度或位置不確定性，許多實驗試圖根據外部環境來測量它。^[ 38 ]

1996 年，巴黎高等師範學院的Serge Haroche和他的同事首次^{定量測量了}^{被退相干逐漸消除的量子疊加}^過程。充滿微波的腔體實現兩種狀態。這兩個量子態都會造成微波場的相位變化，但變化量不同，因此微波場本身也處於兩種狀態的疊加狀態。由於腔鏡缺陷上的光子散射，腔場失去了與環境的相位相干性。 Haroche 和他的同事透過透過空腔發送的原子對狀態之間的相關性（原子之間存在不同的時間延遲）來測量由此產生的退相干。

2011 年 7 月，不列顛哥倫比亞大學和加州大學聖塔芭芭拉分校的研究人員表明，對單分子磁鐵施加高磁場可以抑制三個已知退相干源中的兩個。^[ 40 ]^[ 41 ]^[ 42 ]他們能夠測量退相干對溫度和磁場強度的依賴性。

預防

概念

退相干導致系統失去量子性，使疊加原理失效，並將「量子」變成「經典」。^[ 43 ]這是量子計算的一個重大挑戰。

真實的量子系統不可避免地會遇到周圍環境，這種相互作用在物理過程中表現為雜訊。它對環境雜訊（例如電磁場、溫度波動和其他外部擾動）以及測量極為敏感，會導致退相干。

退相干對於量子電腦的實際實現來說是一個挑戰，因為這種機器預計將嚴重依賴量子相干性的不受干擾的演化。它們要求保持狀態的相干性並管理退相干，以便實際執行量子計算。由於退相干，我們需要在量子位元狀態衰減之前完成量子過程。^[ 44 ]

物理量相干時間定義為量子態保持疊加原理的時間。

抗退相干的目的是延長量子系統的相干時間。它將提高資訊計算的穩定性。^[ 45 ]

方法和工具

研究人員開發了許多方法和工具來減輕或消除退相干的負面影響。下面列出了幾種典型的方式。

與環境隔離

減少退相干最基本、最直接的方法是透過任何類型的隔離來防止量子系統與環境相互作用。以下是這方面的一些典型例子。

高真空：將量子位元放置在超高真空環境中，最大限度地減少與空氣分子的相互作用。^{[需要引用]}
低溫冷卻：在極低的溫度下運作量子系統可減少熱振動和雜訊。^{[需要引用]}
電磁屏蔽：將量子系統封閉在阻擋外部電磁場的材料中，例如高導磁合金或超導材料，可以減少不必要的電磁幹擾所造成的退相干。^{[需要引用]}
屏蔽宇宙射線：2020 年 8 月，科學家報告稱，如果沒有充分屏蔽，來自環境放射性材料和宇宙射線的電離輻射可能會大大限制量子位元的相干時間，這對於未來實現容錯超導量子電腦可能至關重要。^[ 46 ]^[ 47 ]^[ 48 ]
更好的材料：用特殊材料（例如高純度或同位素富集的材料）製造量子位，以最大限度地減少材料的固有噪聲，包括缺陷或核自旋產生的噪聲。^{[需要引用]}
電路設計：設計量子電路結構時最佳化相干能力，類似經典電路中的關注點。^{[需要引用]}
機械和光學隔離：使用隔振台和隔音材料等設備，減少機械噪音源，並屏蔽外部光線——這在物理實驗中很常見。^{[需要引用]}

量子糾錯（QEC）

本文僅參考主要來源。請透過添加第二或第三來源來幫助改進本文。尋找來源：“量子退相干” – 新聞報紙·書籍·學者JSTOR
（2024年 12 月）（了解如何以及何時刪除此訊息）

對抗量子退相干最強大的工具之一是量子糾錯（QEC）。 QEC 方案跨多個物理量子位元對量子資訊進行冗餘編碼，允許在不直接測量量子態的情況下檢測和修正錯誤。這些 QEC 協議依賴於這樣的假設：錯誤在任何給定時間僅影響一小部分量子位，從而能夠透過冗餘編碼來檢測和糾正錯誤。以下是一些代表性的 QEC 協議。

短碼：^[ 49 ]最早的量子糾錯碼之一，它將單一量子位元編碼為九個物理量子位元，以防止位元翻轉和相位翻轉錯誤。

Steane 代碼：^[ 50 ]一種 7 量子位元碼，可為任意錯誤提供糾錯。

表面代碼：^[ 51 ]一種更具可擴展性的糾錯代碼，它使用具有高錯誤閾值的二維量子位點陣。

玻色碼：一種量子糾錯碼，專門設計用於保護連續變數系統中的量子資訊。^{[需要引用]}

然而，QEC 的成本很高：它需要大量的物理量子位元來編碼單一邏輯量子位元，而容錯糾錯方法會引入額外的計算開銷。

動態解耦

動態解耦（DD）是另一種用於對抗退相干的典型量子控制技術，特別是耦合到雜訊環境的系統。 DD 涉及以策略性的時間間隔向量子系統應用外部控制脈衝序列，以平衡環境交互作用。該技術透過外部可控相互作用有效地操縱量子系統與周圍環境相互作用的不可逆成分。^[ 52 ]動態解耦已在各種系統中得到實驗證明，包括捕獲離子^[ 53 ]和超導量子位元。^[ 54 ]以下是一些代表性序列的例子。

自旋回波（SE）：SE由單一π脈衝組成，它反轉系統的狀態。^{[需要引用]}

週期性動態解耦 (PDD)：週期性地施加控制脈衝，PDD 平均化環境的影響並對量子位元進行解耦。^[ 55 ]

Carr-Purcell-Meiboom-Gill (CPMG) 序列：^[ 56 ] CPMG 是 SE 的擴展。它施加一系列 π 脈衝。

參見

沒有留言:

張貼留言

你發現了這篇網誌的留言板，在這留點什麼吧|д･)

訂閱：張貼留言 (Atom)