| 作品 | 基本粒子 |
|---|---|
| 統計數據 | 玻色子 |
| 家庭 | 規範玻色子 |
| 互動 | 電磁、弱(和重力) |
| 象徵 | γ |
| 理論化 | 愛因斯坦 (Albert Einstein) (1905) 「光子」這個名稱通常歸因於吉爾伯特·N·劉易斯 (Gilbert N. Lewis) (1926) |
| 大量的 | 0(理論值) <1 × 10 −18 eV/ c 2(實驗極限)[ 1 ] |
| 平均壽命 | 穩定[ 1 ] |
| 電荷 | 0 <1 × 10 −35 e [ 1 ] |
| 色荷 | 不 |
| 旋轉 | 1 ħ |
| 自旋態 | +1 ħ , −1 ħ |
| 平價 | −1 [ 1 ] |
| C 奇偶校驗 | −1 [ 1 ] |
| 濃縮 | I ( J PC )=0,1( 1 −− ) [ 1 ] |
光子(源自古希臘語φῶς、φωτός ( phôs , phōtós ) 「光」)是一種基本粒子,是電磁場的量子,包括光和無線電波等電磁輻射以及電磁力的力載體。光子是無質量的粒子,其運動速度不會超過真空中測量的光速。光子屬於玻色子粒子一類。
與其他基本粒子一樣,光子最好用量子力學來解釋,並表現出波粒二象性,它們的行為具有波和粒子的特性。[ 2 ]現代光子概念起源於 20 世紀頭二十年阿爾伯特愛因斯坦的工作,他在馬克斯普朗克的研究基礎上發展起來。當普朗克試圖解釋物質和電磁輻射如何彼此保持熱平衡時,他提出,儲存在物質物體中的能量應被視為由整數個離散的、大小相等的部分組成。為了解釋光電效應,愛因斯坦引入了光本身是由離散的能量單位組成的想法。 1926 年,吉爾伯特·N·劉易斯 (Gilbert N. Lewis)推廣了光子這一能量單位的術語。 [ 3 ] [ 4 ] [ 5 ]隨後,許多其他實驗驗證了愛因斯坦的方法。[ 6 ] [ 7 ] [ 8 ]
在粒子物理學的標準模型中,光子和其他基本粒子被描述為物理定律的必然結果,在時空中的每一點都具有一定的對稱性。粒子的內在屬性,例如電荷、質量和自旋,由規範對稱性決定。光子概念帶來了實驗和理論物理學的重大進步,包括雷射、玻色-愛因斯坦凝聚、量子場論和量子力學的機率解釋。它已應用於光化學、高解析度顯微鏡和分子距離測量。此外,光子已作為量子電腦的元素以及在光學成像和光通訊(例如量子密碼學)中的應用進行了研究。
命名法
[編輯]

量子(Quanta,單數量子,拉丁語“多少”的意思)這個詞在 1900 年之前被用來表示粒子或不同量的數量,包括電。 1900年,德國物理學家馬克斯·普朗克正在研究黑體輻射,他提出,如果分子內儲存的能量是“由整數個有限的能量組成的離散量”,那麼實驗觀察結果,特別是在較短波長下的實驗觀察結果就可以得到解釋。[ 9 ] 1905年,阿爾伯特·愛因斯坦發表了一篇論文,其中他提出,透過將電磁波建模為由空間局域的離散能量量子組成,可以更好地解釋許多與光相關的現象,包括黑體輻射和光電效應。 [ 10 ]他稱這些為光量子(德文:ein Lichtquant)。[一]
光子這個名字來自希臘語中的光,φῶς(音譯為phôs)。亞瑟·康普頓 (Arthur Compton)在 1928 年使用了光子,指的是吉爾伯特·N·劉易斯 (Gilbert N. Lewis) ,後者在 1926 年 12 月 18 日寫給《自然》的一封信中創造了這個術語。愛爾蘭物理學家John Joly提出,1924 年由法國生理學家 René Wurmser(1890-1993)提出,1926 年由法國物理學家 Frithiof Wolfers(1891-1971)提出。[ 5 ]該名稱最初是作為與眼睛的照明和由此產生的光感相關的單位而提出的,後來在生理學背景下使用。儘管沃爾弗斯和劉易斯的理論與許多實驗相矛盾並且從未被接受,但康普頓使用這個新名稱後很快就被大多數物理學家採用。[ 5 ] [ b ]
在物理學中,光子通常以符號γ(希臘字母 gamma)表示。這個光子的符號可能源自伽馬射線,伽馬射線由Paul Villard於 1900 年發現,[ 13 ] [ 14 ]由Ernest Rutherford於 1903 年命名,並於 1914 年被 Rutherford 和Edward Andrade證明是電磁輻射的一種形式。[ 15 ]在化學和光學工程中,光子通常用hν來表示,即光子能量,其中h是普朗克常數,希臘字母ν ( nu )是光子的頻率。[ 16 ]
物理特性
[編輯]光子不帶電荷,[ 17 ] [ 18 ]一般被認為具有零靜止質量[ 19 ],是一種穩定的粒子。光子質量的實驗上限[ 20 ] [ 21 ]非常小,約10 -50 kg;其使用壽命將超過10 18年。[ 22 ]作為比較,宇宙的年齡約為 1.38 × 10 10年。
在真空中,光子有兩種可能的偏振態。[ 23 ]光子是電磁學的規範玻色子,[ 24 ]:29-30 ,因此光子的所有其他量子數(例如輕子數、重子數和風味量子數)都為零。[ 25 ]此外,光子服從玻色愛因斯坦統計,而不是費米-狄拉克統計。也就是說,它們不遵守泡利不相容原理[ 26 ]:1221 ,並且多個可以佔據相同的束縛量子態。
許多自然過程都會發射光子。例如,當電荷加速時,它會發出同步加速器輻射。在分子、原子或核躍遷到較低能階的過程中,會發射各種能量的光子,從無線電波到伽瑪射線。當粒子及其相應的反粒子湮滅(例如,電子-正電子湮滅)時,也可以發射光子。[ 26 ]:572、1114、1172
相對論能量和動量
[編輯]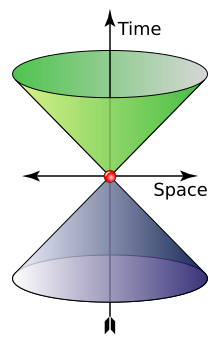
在真空中,光子以c(光速)運動,其能量和動量的關係為E = pc,其中p是動量向量p的大小。這源自於以下相對論關係,其中m = 0:[ 27 ]
光子的能量和動量僅取決於其頻率() 或相反,其波長( λ ):
其中k是波矢量,其中
自從指向光子傳播的方向,其動量大小為
極化和自旋角動量
[編輯]光子還帶有自旋角動量,這與光子偏振有關。 (光束也表現出被描述為光的軌道角動量的特性)。
光子的角動量有兩個可能的值,+ħ或-ħ。這兩個可能的值對應於圓偏振的兩種可能的純狀態。光束中的光子集合可能具有這兩個值的混合;線偏振光束的作用就好像它是由相等數量的兩個可能的角動量組成的。[ 29 ]:325
光的自旋角動量不依賴其頻率,並於1931年由CV Raman和S. Bhagavantam經實驗證實。
反粒子湮滅
[編輯]粒子與其反粒子的碰撞可以產生光子。在自由空間中,必須至少產生兩個光子,因為在動量框架的中心,碰撞的反粒子沒有淨動量,而單一光子總是具有動量(由光子的頻率或波長決定,不能為零)。因此,動量守恆(或等效的平移不變性)要求至少創建兩個淨動量為零的光子。[ c ] [ 31 ] : 64–65 兩光子的能量,或等效地,它們的頻率,可以透過四動量守恆來決定。
從另一個角度來看,光子可以被視為它自己的反粒子(因此「反光子」只是一個具有相反動量、相等偏振和 180° 異相的正常光子)。相反的過程,即電子對產生,是高能量光子(例如伽馬射線)在穿過物質時損失能量的主要機制。[ 32 ]此過程與原子核電場中允許的「湮滅為一個光子」相反。
電磁輻射能量和動量的經典公式可以用光子事件重新表達。例如,物體上電磁輻射的壓力源自於每單位時間和單位面積的光子動量向該物體的轉移,因為壓力是每單位面積的力,而力是每單位時間動量的變化。[ 33 ]
光子質量的實驗檢查
[編輯]目前普遍接受的物理理論暗示或假設光子是嚴格無質量的。如果光子不是完全無質量的,它們的速度會隨頻率而變化,能量較低(較紅)的光子比能量較高的光子移動得稍慢。相對論不會受此影響。那麼,所謂的光速c就不是光移動的實際速度,而是自然常數,它是任何物體理論上在時空中可以達到的速度的上限。 [ 34 ]因此,它仍然是時空漣漪(重力波和重力子)的速度,但它不會是光子的速度。
如果光子確實具有非零質量,也會產生其他效應。庫侖定律將被修改,電磁場將具有額外的物理自由度。這些效應產生比光速的頻率依賴性更靈敏的光子質量實驗探針。如果庫侖定律不完全有效,那麼當空心導體受到外部電場作用時,空心導體體內就會存在電場。這為庫侖定律的精確檢驗提供了手段。[ 35 ]此類實驗的無效結果設定了m ≲的限制10 -14 eV/ c 2。 [ 36 ]
在旨在檢測銀河矢量勢引起的效應的實驗中,已經獲得了更明確的光質量上限。儘管由於星系磁場存在於大長度尺度上,星係向量勢很大,但如果光子無質量,則只能觀測到磁場。如果光子有質量,則質量項12 m 2 A μ A μ會影響銀河等離子體。沒有看到這種效應的事實意味著光子質量的上限為m <3 × 10 -27 eV/ c 2。 [ 37 ]銀河向量勢也可以透過測量施加在磁化環上的扭矩來直接探測。 [ 38 ]此類方法用於獲得更清晰的上限1.07 × 10 −27 eV/ c 2(相當於10 -36 道爾頓)由粒子資料組給出。[ 39 ]
這些由於未觀測到銀河向量勢所造成的影響而產生的尖銳限制已被證明是依賴模型的。[ 40 ]如果光子質量是透過希格斯機制產生的,則m的上限≲由庫侖定律檢驗得到的 10 −14 eV/ c 2是有效的。
歷史發展
[編輯]
在十八世紀之前的大多數理論中,光被描述為由粒子組成。由於粒子模型無法輕易解釋光的折射、繞射和雙折射, René Descartes (1637)、[ 41 ] Robert Hooke (1665)、[ 42 ]和Christiaan Huygens (1678)提出了光的波動理論; [ 43 ]然而,粒子模型仍然占主導地位,這主要是由於艾薩克·牛頓的影響。[ 44 ] 19世紀初,托馬斯·楊和奧古斯特·菲涅爾清楚地證明了光的干涉和衍射,到1850年波模型被普遍接受。[ 45 ] 詹姆斯·克拉克·麥克斯韋1865 年的預測[ 46 ]認為光是一種電磁波——這一點在 1888 年通過海因里希·赫茲對無線電波的探測得到了實驗證實[ 47 ] ——似乎是對光粒子模型的最後一擊。
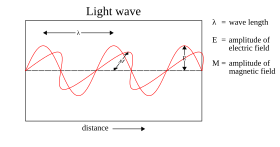
然而,麥克斯韋波理論並沒有解釋光的所有屬性。麥克斯韋理論預測光波的能量只取決於其強度,而不取決於其頻率。然而,幾種獨立類型的實驗表明,光傳遞給原子的能量僅取決於光的頻率,而不取決於其強度。例如,某些化學反應只有頻率高於某個閾值的光才能引發;頻率低於閾值的光,無論多麼強烈,都不會引發反應。類似地,透過將足夠高頻率的光照射到金屬板上,電子可以從金屬板上發射出來(光電效應);噴射電子的能量僅與光的頻率有關,與其強度無關。[ 48 ] [ d ]
同時,不同的研究人員對黑體輻射進行了四十年(1860-1900)的研究[ 50 ],最終得出了馬克斯·普朗克的假設[ 51 ] [ 52 ] ,即任何吸收或發射能量的系統頻率為ν是能量量子E = hν的整數倍。正如阿爾伯特·愛因斯坦所指出的,[ 10 ] [ 53 ]必須假設某種形式的能量量子化能夠解釋物質和電磁輻射之間觀察到的熱平衡。由於對光電效應的這種解釋,愛因斯坦獲得了 1921 年諾貝爾物理學獎。[ 54 ]
由於麥克斯韋光理論允許電磁輻射的所有可能能量,因此大多數物理學家最初假設能量量子化是由吸收或發射輻射的物質的某些未知限制引起的。 1905年,愛因斯坦第一個提出能量量子化是電磁輻射本身的特性。[ 10 ]儘管愛因斯坦承認麥克斯韋理論的有效性,但他指出,如果麥克斯韋光波的能量被局域化為彼此獨立運動的點狀量子,那麼許多反常實驗就可以得到解釋,即使波本身是不斷地擴散到空間之中。[ 10 ]在 1909 年[ 53 ]和 1916 年,[ 55 ]愛因斯坦證明,如果普朗克關於黑體輻射的定律被接受,能量量子也必須攜帶動量 p = 小時 λ ,使它們成為成熟的粒子。亞瑟·康普頓 (Arthur Compton透過實驗觀察到了這種光子動量, [ 56 ],他因此於1927 年獲得了諾貝爾獎。的粒子性質統一起來。這個問題的答案佔據了阿爾伯特·愛因斯坦的餘生, [ 57 ]並在量子電動力學及其後繼者標準模型中得到了解決。 (參見下文§量子場論和§作為規範玻色子。)

愛因斯坦 1905 年的預言在 20 世紀的前二十年裡通過多種方式得到了實驗驗證,正如羅伯特·密立根 (Robert Millikan)的諾貝爾獎演講中所敘述的那樣。[ 58 ]然而,在康普頓的實驗[ 56 ]顯示光子攜帶與其波數成正比的動量之前(1922年),[需要完整引用]大多數物理學家不願意相信電磁輻射本身可能是微粒的。 (例如,請參閱維恩、[ 50 ]普朗克[ 52 ]和密立根的諾貝爾演講。)[ 58 ]相反,人們普遍認為能量量子化是由於吸收或發射輻射的物質受到某種未知的約束而產生的。隨著時間的推移,態度也發生了變化。在某種程度上,這種變化可以追溯到那些揭示康普頓散射的實驗,在這些實驗中,不將量子化歸因於光本身來解釋觀察到的結果要困難得多。[ 59 ]
即使在康普頓的實驗之後,尼爾斯·玻爾(Niels Bohr)、亨德里克·克萊默斯(Hendrik Kramers)和約翰·斯萊特(John Slater)仍進行了最後一次嘗試,以保存光的麥克斯韋連續電磁場模型,即所謂的BKS 理論。[ 60 ] BKS理論的一個重要特點是它如何處理能量守恆和動量守恆。在 BKS 理論中,能量和動量僅在物質與輻射之間的許多相互作用中平均守恆。然而,精確的康普頓實驗表明,守恆定律對於個體相互作用是成立的。[ 61 ]因此,玻爾和他的同事為他們的模特兒舉行了「盡可能尊貴的葬禮」。[ 57 ]儘管如此,BKS 模型的失敗激發了維爾納·海森堡對矩陣力學的發展。[ 62 ]
一些物理學家堅持[ 63 ]發展半經典模型,其中電磁輻射未被量子化,但物質似乎遵守量子力學定律。儘管到 20 世紀 70 年代,來自化學和物理實驗的證明光子存在的證據已是壓倒性的,但這些證據不能被認為是絕對確定的;因為它依賴光與物質的相互作用,並且足夠完整的物質理論原則上可以解釋這些證據。然而,所有半經典理論在 20 世紀 70 年代和 80 年代都被光子相關實驗徹底駁倒。[ e ]因此,愛因斯坦關於量子化是光本身的屬性的假設被認為得到了證明。
波粒二象性和不確定性原理
[編輯]光子遵循量子力學定律,因此它們的行為既有波狀又有粒子狀。當測量儀器檢測到光子時,它被記錄為單一顆粒單元。然而,檢測到光子的機率是透過描述波的方程式計算的。這種面向的組合稱為波粒二象性。例如,可能檢測到光子的位置的機率分佈清楚地顯示出類似波的現象,例如衍射和乾涉。透過雙縫的單一光子在螢幕上的一點接收到其能量,其機率分佈由麥克斯韋波動方程式確定的干涉圖案給出。[ 66 ]然而,實驗證實光子不是電磁輻射的短脈衝;光子的麥克斯韋波會發生衍射,但光子能量在傳播時不會擴散,當遇到分束器時能量也不會分裂。[ 67 ]相反,接收到的光子的行為就像點狀粒子,因為它被任意小的系統吸收或發射作為一個整體,包括比其波長小得多的系統,例如原子核(直徑約10 -15 m )甚至是點狀電子。
雖然許多介紹性文本使用非相對論量子力學的數學技術來處理光子,但這在某種程度上是一種尷尬的過度簡化,因為光子本質上是相對論性的。由於光子的靜止質量為零,因此為光子定義的波函數不能具有非相對論量子力學中波函數所熟悉的所有屬性。[ f ]為了避免這些困難,物理學家採用了下面描述的光子的第二個量子化理論,即量子電動力學,其中光子是電磁模式的量子化激發。[ 72 ]
另一個困難是為不確定性原理找到合適的類比,這個想法經常被認為是海森堡提出的,他在分析涉及電子和高能量光子的思想實驗時引入了這個概念。然而,海森堡並沒有對這些測量中的「不確定性」給出精確的數學定義。位置動量不確定原理的精確數學表述歸功於Kennard、Pauli和Weyl。[ 73 ] [ 74 ]不確定性原理適用於實驗者可以選擇測量兩個「正則共軛」量之一的情況,例如粒子的位置和動量。根據不確定性原理,無論粒子如何準備,都不可能對這兩種替代測量進行精確預測:如果使位置測量的結果更加確定,則動量測量的結果就變得更加確定則不然,反之亦然。[ 75 ]在量子力學允許的範圍內,相干態可以最大限度地減少整體不確定性。[ 72 ]量子光學利用電磁場模式的相干態。在電磁波振幅和相位的測量之間存在著一種權衡,讓人聯想到位置動量不確定性關係。[ 72 ]這有時非正式地表達為電磁波中存在的光子數量的不確定性, ,以及波相位的不確定性,。然而,這不可能是 Kennard-Pauli-Weyl 類型的不確定關係,因為與位置和動量不同,相位不能用Hermitian 算符表示。[ 76 ]
光子氣體的玻色愛因斯坦模型
[編輯]1924 年,Satyendra Nath Bose在沒有使用任何電磁學的情況下,而是透過對相空間的粗粒度計數進行修改,推導出了普朗克黑體輻射定律。[ 77 ]愛因斯坦表明,這種修改相當於假設光子是嚴格相同的,並且它意味著“神秘的非局域相互作用”,[ 78 ] [ 79 ]現在被理解為對稱量子力學狀態的要求。這項工作導致了相干態的概念和雷射的發展。在同一篇論文中,愛因斯坦將玻色的形式主義擴展到物質粒子(玻色子),並預測它們會在足夠低的溫度下凝結成最低的量子態;這種玻色愛因斯坦凝聚在1995年被實驗觀察到。
現代觀點認為,光子由於其整數自旋而成為玻色子(與具有半整數自旋的費米子相反)。根據自旋統計定理,所有玻色子都服從玻色-愛因斯坦統計(而所有費米子服從費米-狄拉克統計)。[ 83 ]
受激發射和自發發射
[編輯]
1916 年,阿爾伯特愛因斯坦證明,普朗克輻射定律可以從光子和原子的半經典統計處理中推導出來,這意味著原子發射和吸收光子的速率之間存在關聯。此條件源自以下假設:原子的輻射發射和吸收函數彼此獨立,並且透過輻射與原子的相互作用實現熱平衡。考慮一個與其自身所有部分處於熱平衡狀態並充滿電磁輻射的空腔,並且原子可以發射和吸收該輻射。熱平衡要求能量密度光子的頻率(與它們的數量密度成正比)平均而言是隨時間變化的;因此,任何特定頻率的光子發射速率必須等於它們被吸收的速率。[ 84 ]
愛因斯坦首先假設所涉及的不同反應速率的簡單比例關係。在他的模型中,比率用於吸收頻率光子的系統以及從較低能量的轉變到更高的能量與數量成正比具有能量的原子和能量密度該頻率的環境光子,
在哪裡是吸收速率常數。對於相反的過程,有兩種可能性:光子的自發性發射,或由原子與經過的光子相互作用引發的光子發射以及原子返回到較低能態。按照愛因斯坦的方法,相應的速率用於發射頻率光子以及從更高能量的轉變到較低的能量是
在哪裡是自發發射光子的速率常數,並且是響應環境光子(感應或受激發射)的發射速率常數。在熱力學平衡中,處於狀態的原子數以及那些處於狀態的人平均而言,必須是恆定的;因此,費率和必須相等。此外,透過類似玻爾茲曼統計推導的論證,和是在哪裡和是國家的墮落以及, 分別,和他們的能量,波茲曼常數和系統的溫度。由此,不難得出
和
這和統稱為愛因斯坦係數。[ 85 ]
愛因斯坦無法完全證明他的速率方程,但聲稱應該可以計算係數,和一旦物理學家獲得了「為適應量子假說而修改的力學和電動力學」。[ 86 ]此後不久,1926 年,保羅狄拉克 (Paul Dirac)推導出透過使用半經典方法來研究速率常數,[ 87 ],並於 1927 年成功地從量子理論框架內的第一原理推導出所有速率常數。 [ 88 ] [ 89 ]狄拉克的工作是量子電動力學的基礎,即電磁場本身的量子化。狄拉克的方法也稱為第二量子化或量子場論;[ 90 ] [ 91 ] [ 92 ]早期的量子力學處理僅將材料粒子視為量子力學,而非電磁場。
愛因斯坦對他的理論似乎不完整這一事實感到困擾,因為它無法確定自發性發射光子的方向。牛頓在處理雙折射時首先考慮了光粒子運動的機率性質,更一般地說,在處理界面處的光束分裂為透射光束和反射光束時。牛頓假設光粒子中的隱藏變數決定了單一光子將採取兩條路徑中的哪一條。[ 44 ]同樣,愛因斯坦希望有一個更完整的理論,不留任何機會,從而開始與量子力學分離[ 57 ]。諷刺的是,馬克斯·玻恩對波函數的機率解釋[ 93 ] [ 94 ]受到了愛因斯坦後來尋找更完整理論的工作的啟發。[ 95 ]
量子場論
[編輯]電磁場的量子化
[編輯]
1910 年,彼得‧德拜 (Peter Debye)從一個相對簡單的假設推導出了普朗克黑體輻射定律。 [ 96 ]他將空腔內的電磁場分解為其傅立葉模式,並假設任何模式下的能量都是以下的整數倍:, 在哪裡是電磁模式的頻率。普朗克黑體輻射定律立即遵循幾何和。然而,德拜的方法未能給出黑體輻射能量漲落的正確公式,該公式是愛因斯坦在1909年導出的。
1925年,玻恩、海森堡和喬丹對德拜的概念進行了關鍵性的重新詮釋。[ 97 ]如經典所示,電磁場的傅立葉模式(由波向量k和偏振態索引的一組完整的電磁平面波)相當於一組非耦合簡諧振子。經過量子力學處理,這種振盪器的能階已知為, 在哪裡是振盪器頻率。關鍵的新步驟是識別具有能量的電磁模式作為一個國家光子,每個能量。這種方法給出了正確的能量漲落公式。

狄拉克在這一點上更進了一步。[ 88 ] [ 89 ]他將電荷和電磁場之間的相互作用視為一個小擾動,該擾動會引起光子狀態的轉變,改變模式中的光子數量,同時總體上守恆能量和動量。狄拉克能夠推導出愛因斯坦的和係數,並顯示光子的玻色愛因斯坦統計是正確量化電磁場的自然結果(玻色的推理走向相反的方向;他透過假設B-E 統計推導出普朗克黑體輻射定律) 。在狄拉克時代,人們還不知道所有玻色子,包括光子,都必須服從玻色-愛因斯坦統計。
狄拉克的二階微擾理論可以涉及虛擬光子、電磁場的瞬態中間態;靜電和磁性相互作用是由這種虛擬光子介導的。在這種量子場論中,可觀測事件的機率幅度是透過對所有可能的中間步驟(甚至是非物理步驟)求和來計算的;因此,虛光子不限於滿足,並且可能有額外的偏振態;根據所使用的規範,虛擬光子可能具有三個或四個偏振態,而不是真實光子的兩個狀態。儘管這些瞬態虛擬光子永遠無法被觀測到,但它們對可觀測事件的機率做出了可測量的貢獻。[ 98 ]
事實上,這種二階和高階微擾計算顯然可以對總和做出無限的貢獻。這種非物理結果可以使用重整化技術進行修正。[ 99 ]
其他虛粒子也可能對求和有貢獻;例如,兩個光子可以透過虛擬電子-正電子 對間接相互作用。[ 100 ]這種光子-光子散射(參見雙光子物理學)以及電子-光子散射是計畫中的粒子加速器(國際直線對撞機)的運作模式之一。[ 101 ]
在現代物理符號中,電磁場的量子態被寫為福克態,它是每種電磁模式的狀態的 張量積
在哪裡代表以下狀態光子處於模式。在這種表示法中,在模式下創建一個新光子(例如,從原子躍遷發出)寫為。這種表示法僅僅表達了上述玻恩、海森堡和喬丹的概念,並沒有添加任何物理學。
作為規範玻色子
[編輯]電磁場可以理解為規範場,即要求時空中每個位置獨立保持規範對稱性而產生的場。[ 102 ]對於電磁場,這種規範對稱性是絕對值為1的複數的阿貝爾 U(1)對稱性,它反映了改變複數場的相位而不影響可觀測量或由其構成的實值函數的能力,例如能量或拉格朗日。
只要對稱性不破缺,阿貝爾規範場的量子就必須是無質量、不帶電的玻色子;因此,光子預計是無質量的,並且具有零電荷和整數自旋。電磁相互作用的特定形式規定光子的自旋必須為±1;因此,它的螺旋度必須是。這兩個自旋分量對應於右手和左手圓偏振光的經典概念。然而,量子電動力學的瞬態虛擬光子也可能採用非物理偏振態。[ 102 ]
在流行的物理學標準模型中,光子是電弱相互作用中的四種規範玻色子之一;其他三個表示為 W +、W −和 Z 0,負責弱相互作用。與光子不同,這些規範玻色子具有質量,這是由於一種打破其SU(2) 規範對稱性的機制。Sheldon Glashow、Abdus Salam和Steven Weinberg在電弱相互作用中實現了光子與 W 和 Z 規範玻色子的統一,並因此獲得了 1979 年諾貝爾物理學獎。[ 103 ] [ 104 ] [ 105 ]物理學家繼續假設大統一理論,將這四種規範玻色子與量子色動力學的八種膠子規範玻色子連結起來;然而,這些理論的關鍵預測,例如質子衰變,尚未透過實驗觀察到。[ 106 ]
強子特性
[編輯]對高能量光子和強子之間相互作用的測量表明,這種相互作用比僅光子與強子電荷的相互作用所預期的要強烈得多。此外,儘管質子和中子的電荷結構本質上不同,但高能量光子與質子的相互作用類似於光子與中子的相互作用[ 107 ] 。一種稱為向量介子優勢(VMD)的理論被發展來解釋這種效應。根據 VMD,光子是純電磁光子(僅與電荷相互作用)和向量介子(介導殘餘核力)的疊加。[ 108 ]然而,如果在非常短的距離上進行實驗探測,光子的內在結構似乎具有夸克和膠子的電荷中性通量作為組成部分,根據QCD中的漸近自由,它是準自由的。此通量由光子結構函數描述。[ 109 ] [ 110 ] Nisius (2000)的評論提出了數據與理論預測的全面比較。[ 111 ]
對系統品質的貢獻
[編輯]發射光子的系統的能量會因能量而減少在發射系統的其餘框架中測量的光子的數量,這可能會導致質量的減少。類似地,吸收光子的系統的質量也會增加相應的量。作為一種應用,涉及光子的核反應的能量平衡通常用所涉及的原子核的質量來表示,並且術語為對於伽馬光子(以及其他相關能量,例如原子核的反沖能)。[ 112 ]
這個概念應用於量子電動力學(QED,見上文)的關鍵預測。在該理論中,電子(或更一般地說,輕子)的質量透過包含虛擬光子的質量貢獻來修改,這種技術稱為重整化。這種「輻射校正」有助於 QED 的許多預測,例如輕子的磁偶極矩、蘭姆位移以及束縛輕子對(例如μ和正電子)的超精細結構。[ 113 ]
根據廣義相對論,由於光子對應力-能量張量有貢獻,因此它們會對其他物體施加引力。相反,光子本身會受到重力的影響。它們通常筆直的軌跡可能會因扭曲的時空而彎曲,例如重力透鏡效應,並且它們的頻率可能會因移動到更高的引力位勢而降低,例如龐德-雷布卡實驗。然而,這些效應並不是光子所特有的。對於經典電磁波,也可以預測出完全相同的效應。[ 114 ]
就事論
[編輯]光穿過透明物質的速度低於c(真空中的光速)。速度降低的因素稱為材料的折射率。在經典的波動圖中,減慢可以透過光在物質中引起電極化、偏振物質輻射新光以及新光與原始光波干涉形成延遲波來解釋。在粒子影像中,減速可以描述為光子與物質的量子激發的混合,產生稱為極化子的準粒子。極化子具有非零有效質量,這意味著它們不能以c傳播。不同頻率的光可能以不同的速度穿過物質;這稱為色散(不要與散射混淆)。在某些情況下,它可能會導致物質中的光速極慢。光子與其他準粒子相互作用的影響可以在拉曼散射和布里淵散射中直接觀察到。[ 115 ]
光子可以被物質散射。例如,光子離開太陽核心後在太陽輻射區散射多次,輻射能需要大約一百萬年才能到達對流區。[ 116 ]然而,從太陽光球層發射的光子只需8.3分鐘即可到達地球。[ 117 ]
光子也可以被原子核、原子或分子吸收,引發它們的能階之間的躍遷。一個典型的例子是視網膜(C 20 H 28 O)的分子轉變,它負責視覺,由諾貝爾獎得主生物化學家 George Wald及其同事於 1958 年發現。吸收引起順反 異構化,與其他此類轉變結合,轉化為神經衝動。光子的吸收甚至可以破壞化學鍵,如氯的光解;這是光化學的主題。[ 118 ] [ 119 ]
科技應用
[編輯]光子在技術中有許多應用。選擇這些例子是為了說明光子本身的應用,而不是可以在經典光理論下運行的一般光學設備,例如透鏡等。雷射是一種重要的應用,上面已在受激發射下進行了討論。
可以透過多種方法檢測單一光子。經典的光電倍增管利用光電效應:足夠能量的光子撞擊金屬板並撞擊出電子,從而引發不斷放大的電子雪崩。半導體 電荷耦合元件晶片使用類似的效應:入射光子在可偵測到的微型電容器上產生電荷。其他偵測器(例如蓋革計數器)則利用光子電離設備中所含氣體分子的能力,導致氣體電導率發生可偵測的變化。 [ 120 ]
普朗克能量公式工程師和化學家在設計中經常使用它,既可以計算光子吸收引起的能量變化,也可以確定給定光子發射所發出的光的頻率。例如,氣體放電燈的發射光譜可以透過填充具有不同電子能階配置的氣體(混合物)來改變。[ 121 ]
在某些條件下,能量躍遷可以由「兩個」光子激發,而單獨的光子是不夠的。這允許更高解析度的顯微鏡,因為樣品僅吸收不同顏色的兩束明顯重疊的光譜中的能量,這可以比單束的激發體積小得多(參見雙光子激發顯微鏡)。此外,這些光子對樣品造成的損害較小,因為它們的能量較低。[ 122 ]
在某些情況下,兩個能量躍遷可以耦合,這樣,當一個系統吸收光子時,附近的另一個系統「竊取」其能量並重新發射不同頻率的光子。這是螢光共振能量轉移的基礎,螢光共振能量轉移是分子生物學中用於研究合適蛋白質相互作用的技術。[ 123 ]
幾種不同類型的硬體隨機數產生器涉及單光子的檢測。在一個範例中,對於要產生的隨機序列中的每一位,將一個光子傳送到分束器。在這種情況下,有兩種可能的結果具有相同的機率。實際結果用於確定序列中的下一位是“0”還是“1”。[ 124 ] [ 125 ]
量子光學與計算
[編輯]許多研究致力於光子在量子光學領域的應用。光子似乎非常適合作為極快量子電腦的元件,而光子的量子糾纏是研究的焦點。非線性光學過程是另一個活躍的研究領域,其主題包括雙光子吸收、自相位調製、調製不穩定性和光學參量振盪器。然而,這樣的過程通常不需要光子本身的假設;它們通常可以透過將原子視為非線性振盪器來建模。自發參量下轉換的非線性過程通常用於產生單光子態。最後,光子在光通訊的某些方面至關重要,特別是對於量子密碼學。[ 126 ]
雙光子物理學研究光子之間的相互作用,這種情況很少見。 2018年,麻省理工學院的研究人員宣布發現了束縛光子三重態,其中可能涉及極化激元。[ 127 ] [ 128 ]











































沒有留言:
張貼留言
Love the Lord your God with all your heart and with all your soul and with all your mind.
耶 穌 對 他 說 : 你 要 盡 心 、 盡 性 、 盡 意 愛 主 ─ 你 的 神 。
—— Matthew 22:37 —— 馬 太 福 音 22:37