貝爾定理是一個包含許多密切相關的物理學結果的術語,所有這些結果都確定量子力學與局部隱變量理論不相容,給出了有關測量本質的一些基本假設。這裡的「局域」是指局域性原理,即粒子只能受到其周圍環境的影響,而物理場介導的相互作用不能以超過光速的速度傳播。 「隱藏變數」是量子粒子的假定屬性,它們不包含在量子理論中,但仍會影響實驗結果。用物理學家約翰·斯圖爾特·貝爾(該系列結果以他的名字命名)的話來說,「如果[隱變量理論]是局域的,那麼它就不會與量子力學一致,而如果它與量子力學一致,那麼它就不是局域的。[ 1 ]
第一個這樣的結果是貝爾在 1964 年基於愛因斯坦-波多爾斯基-羅森悖論提出的,該悖論引起了人們對量子糾纏現象的關注。貝爾推斷,如果對糾纏對中的兩個分離粒子獨立進行測量,那麼結果取決於每一半中的隱藏變數的假設意味著對兩個測量結果如何相關的數學約束。這樣的限制後來被命名為貝爾不等式。貝爾隨後表明,量子物理學預測了違反此不等式的相關性。在接下來的幾年裡,人們提出了貝爾定理的多種變體,使用不同的假設並獲得不同的貝爾(或“貝爾型”)不等式。
約翰·克勞瑟 (John Clauser)和斯圖爾特·弗里德曼 (Stuart Freedman)於 1972 年進行了第一個旨在檢驗貝爾定理的基本實驗。[ 2 ]此後,更先進的實驗(統稱為貝爾測試)已經進行了多次。通常,這些實驗的目標是“堵住漏洞”,即改善原則上可能影響早期貝爾測試結果有效性的實驗設計或設定問題。貝爾測試一致發現物理系統服從量子力學並違反貝爾不等式;也就是說,這些實驗的結果與局部隱變量理論不相容。[ 3 ] [ 4 ]
證明相關性的貝爾型約束所需的假設的確切性質一直受到物理學家和哲學家的爭論。雖然貝爾定理的重要性是毋庸置疑的,但量子力學的不同解釋對於它到底意味著什麼存在分歧。
定理
基本思想有很多變化,其中一些採用了比其他更強的數學假設。[ 5 ]值得注意的是,貝爾型定理並不涉及任何特定的局部隱變量理論,而是顯示量子物理學違反了經典自然圖景背後的一般假設。貝爾在 1964 年證明的原始定理並不是最適合實驗的,用後來的例子來介紹貝爾型不等式的類型很方便。[ 6 ]
假設的人物愛麗絲和鮑伯站在相距很遠的地方。他們的同事維克多準備了一對粒子,並將一個發送給愛麗絲,另一個發送給鮑伯。當愛麗絲收到她的粒子時,她選擇執行兩種可能的測量之一(也許透過擲硬幣來決定哪一個)。將這些測量值表示為和。兩個都和是二進位測量:結果是或者,同樣對於。當鮑勃收到他的粒子時,他選擇兩個測量之一,和,它們也是二進制的。
假設每次測量都揭示了粒子已經擁有的屬性。例如,如果愛麗絲選擇測量並得到結果,那麼她所收到的粒子的值為對於財產。[註1 ]考慮組合因為兩者和取值,那麼要么或者。在前一種情況下,數量必須等於 0,而在後一種情況下,。因此,上述表達式右側的一項將消失,而另一項將等於。因此,如果在維克多準備新的粒子對的情況下重複多次實驗,則組合平均值的絕對值所有試驗中的 都會小於或等於 2 。使用尖括號表示平均值這是貝爾不等式,具體來說是CHSH 不等式。[ 6 ] : 115 這裡的推導取決於兩個假設:首先,基礎物理屬性和獨立於被觀察或測量而存在(有時稱為現實主義假設);其次,愛麗絲的行動選擇不能影響鮑伯的結果,反之亦然(通常稱為局部性假設)。[ 6 ]:117
量子力學可以違反 CHSH 不等式,如下所示。維克多準備了一對量子位,他用貝爾態描述了這對量子位在哪裡和是泡利矩陣之一的本徵態,然後,維克多將第一個量子位元傳遞給愛麗絲,將第二個量子位元傳遞給鮑伯。 Alice 和 Bob 對可能測量的選擇也是根據泡利矩陣定義的。 Alice 測量兩個可觀察量中的一個和:鮑伯測量兩個可觀察量中的一個Victor 可以使用玻恩規則 計算這些可觀測量對的量子期望值:雖然在一次實驗中只能進行這四種測量中的一種,但總和給出 Victor 期望在多個試驗中找到的平均值的總和。該值超過了根據局部隱變量假設推導出來的經典上限 2。[ 6 ]:116 值事實上, 是量子物理學允許的最大期望值組合,使其成為Tsirelson 界。[ 9 ]:140
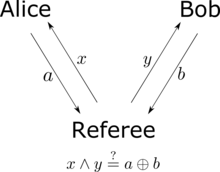
CHSH 不等式也可以被認為是Alice 和 Bob 試圖協調他們的行動的遊戲。[ 10 ] [ 11 ] Victor 準備兩位,和,獨立且隨機。他發送比特給愛麗絲和比特給鮑伯。如果愛麗絲和鮑伯返回答案位,則他們獲勝和對維克多來說,滿足或者,等價地,如果以下邏輯與,則 Alice 和 Bob 獲勝和是邏輯異或和。 Alice 和 Bob 可以在遊戲前就他們想要的任何策略達成一致,但一旦遊戲開始,他們就無法進行交流。在任何基於局部隱變數的理論中,Alice 和 Bob 獲勝的機率都不大於,無論他們事先同意什麼策略。然而,如果他們共享糾纏量子態,他們獲勝的機率可能會大到
變化及相關結果
貝爾 (1964)
貝爾1964年的論文指出,在受限條件下,局部隱變數模型可以重現量子力學的預測。然後他證明這在一般情況下是不成立的。[ 12 ]貝爾考慮了大衛·博姆 (David Bohm)對愛因斯坦-波多爾斯基-羅森 (EPR) 思想實驗的改進。在這種情況下,一對粒子以自旋單重態(這是糾纏態的一個例子)所描述的方式一起形成。然後粒子向相反的方向移動。每個粒子都由Stern–Gerlach 裝置測量,這是一種可以定向在不同方向並報告兩種可能結果之一的測量儀器,可表示為和。每個測量儀器的配置由一個單位向量表示,並透過設定對兩個探測器之間的相關性進行量子力學預測和是特別是,如果兩個偵測器的方向相同(),那麼一個測量的結果肯定是另一個測量結果的負數,給出。如果兩個偵測器的方向正交(),那麼結果是不相關的,並且。貝爾透過例子證明了這些特殊情況可以用隱變數來解釋,然後繼續證明涉及中間角的全部可能性都不能解釋。
貝爾假設,這些相關性的局部隱藏變數模型可以用某些隱藏參數的可能值的積分來解釋它們:在哪裡是機率密度函數。兩個函數和提供給定方向向量和隱藏變數的兩個偵測器的響應:至關重要的是,探測器的結果不依賴於,同樣的結果不依賴於,因為兩個探測器在物理上是分開的。現在我們假設實驗者可以選擇第二個偵測器的設定:它可以設定為或到。貝爾證明了這兩種探測器設定選擇之間的相關性差異必須滿足不等式然而,很容易發現量子力學違反貝爾不等式的情況。[ 13 ] : 425–426 例如,讓向量和是正交的,並且讓位於與它們兩者成 45° 角的平面上。然後儘管但因此,不存在局部隱變數模型可以重現量子力學對所有選擇的預測。,, 和只要考慮到實驗的缺陷,實驗結果就會與經典曲線相矛盾,並與量子力學預測的曲線相符。[ 5 ]
貝爾 1964 年定理需要完美反相關的可能性:在知道第一個偵測器的結果的情況下,能夠對第二個偵測器的結果進行機率 1 預測。這與「EPR現實標準」有關,這是愛因斯坦、波多爾斯基和羅森在1935年論文中提出的概念。本文假設:“如果在不以任何方式乾擾系統的情況下,我們可以確定地(即機率等於一)預測一個物理量的值,那麼就存在與該量相對應的現實元素。” [ 14 ]
GHZ-梅爾敏 (1990)
Daniel Greenberger、Michael A. Horne和Anton Zeilinger在 1990 年提出了一個四粒子思想實驗,隨後David Mermin將其簡化為僅使用三個粒子。[ 15 ] [ 16 ]在這個思想實驗中,Victor 產生了一組由量子態描述的三個自旋 1/2 粒子如上所述,和是泡利矩陣的特徵向量。然後,維克多向愛麗絲、鮑伯和查理各發送一個粒子,他們在相距很遠的地點等待。愛麗絲測量任一或者在她的粒子上,鮑伯和查理也是如此。每次測量的結果是或者。將玻恩規則應用於三量子位元狀態,Victor 預測每當三個測量值包含一個和兩個的,結果的乘積永遠是。這是因為是一個特徵向量具有特徵值,同樣對於和。因此,知道 Alice 的結果測量和鮑勃的結果測量,Victor 可以以機率 1 預測 Charlie 將回傳什麼結果測量。根據 EPR 的現實標準,將會有一個「現實要素」對應於某個結果。查理量子位的測量。事實上,同樣的邏輯也適用於測量和所有三個量子位元。那麼,根據現實的 EPR 標準,每個粒子都包含一個“指令集”,它決定了一個粒子的結果。或者對其進行測量。然後,所有三個粒子的集合將由指令集描述每個條目都是或者,以及每個或者測量只是傳回適當的值。
如果愛麗絲、鮑伯和查理都執行測量,那麼他們的結果的乘積將是。該值可以從因為任一的平方或者是。括號中的每個因數等於, 所以Alice、Bob 和 Charlie 結果的乘積將是具有機率統一。但這與量子物理學不一致:Victor 可以使用狀態來預測即測量相反會產生具有機率統一。
這個思想實驗也可以改寫為傳統的貝爾不等式,或者等同地,改寫為與 CHSH 博弈精神相同的非局部博弈。[ 17 ]其中,愛麗絲、鮑伯和查理接收比特來自 Victor 的承諾,總是有偶數個,即,並向他發回位。他們贏得比賽,如果所有輸入都有奇數個 1,除了,當他們需要有偶數個時。也就是說,他們贏得比賽當且僅當。使用局部隱藏變量,他們獲勝的最高機率是 3/4,而使用上面的量子策略,他們可以確定獲勝。這是量子偽心靈感應的一個例子。
科亨-斯佩克定理 (1967)
在量子理論中,希爾伯特空間的正交基底表示可以在具有該希爾伯特空間的系統上執行的測量。基底中的每個向量代表該測量的可能結果。[註2 ]假設一個隱藏變數存在,以便了解其價值意味著任何測量結果的確定性。給定值為,每個測量結果——即希爾伯特空間中的每個向量——要么是不可能的,要么是有保證的。Kochen-Specker 配置是由多個互鎖基底組成的有限向量集,具有這樣的屬性:當被認為屬於一個基底時,其中的向量總是不可能的,而當被認為屬於另一個基底時,則保證向量。換句話說,Kochen-Specker 配置是一個“不可著色集”,它證明了假設隱藏變數的不一致可以控制測量結果。[ 22 ]:196–201
自由意志定理
Kochen-Specker 類型的論證,使用互鎖基底的配置,可以與測量貝爾型不等式背後的糾纏對的想法相結合。 Kochen、 [ 23 ] Heywood 和 Redhead、[ 24 ] Stairs、[ 25 ]以及 Brown 和 Svetlichny在 20 世紀 70 年代就注意到了這一點。 [ 26 ]正如EPR所指出的,獲得糾纏對的一半的測量結果意味著另一半的相應測量結果的確定性。 「EPR 現實標準」假設,由於該對的後半部沒有受到干擾,因此這種確定性一定是由於屬於它的物理屬性。[ 27 ]換句話說,根據這個標準,隱藏變數必須存在於該對的第二個、尚未測量的一半內。如果僅考慮上半部的一個測量,則不會產生矛盾。然而,如果觀察者可以選擇多個可能的測量值,並且定義這些測量值的向量形成 Kochen-Specker 配置,那麼後半部的某些結果將同時是不可能的和保證的。
當約翰·康威(John Conway)和西蒙·科亨(Simon Kochen)以自由意志定理的名義提出此類論證的實例時,這種論證引起了人們的關注。[ 28 ] [ 29 ] [ 30 ]康威-科亨定理使用一對糾纏四維體與阿舍‧佩雷斯所發現的科亨-斯佩克構型。[ 31 ]
準經典糾纏
正如貝爾所指出的,量子力學的一些預測可以在局部隱變量模型中複製,包括由糾纏產生的相關性的特殊情況。自從貝爾定理誕生以來,這個主題已經被系統性地研究了很多年。 1989 年,Reinhard Werner引入了現在所謂的Werner 態,這是一對系統的聯合量子態,它產生 EPR 型相關性,但也承認隱變量模型。[ 32 ]維爾納態是二部量子態,在對稱張量積形式的么正下不變:2004 年,Robert Spekkens引入了一個玩具模型,該模型以局部離散自由度為前提,然後施加“知識平衡原則”,限制觀察者對這些自由度的了解程度,從而使它們成為隱藏變數。關於基礎變數(「本體狀態」)的允許的知識狀態(「認知狀態」)模仿了量子態的某些特徵。玩具模型中的相關性可以模擬糾纏的某些方面,例如一夫一妻制,但透過構造,玩具模型永遠不會違反貝爾不等式。[ 33 ] [ 34 ]
歷史
背景
量子力學是否可以透過隱變數「完善」的問題可以追溯到量子理論的早期。出生於匈牙利的博學者約翰·馮·諾依曼在其1932 年出版的量子力學教科書中提出了他聲稱的證明,即不存在「隱藏參數」。馮·諾依曼證明的有效性和確定性受到了漢斯·賴辛巴赫的質疑,更詳細地受到了格蕾特·赫爾曼的質疑,並且可能在談話中受到了阿爾伯特·愛因斯坦的質疑,儘管沒有發表出來。[註3 ](Simon Kochen和Ernst Specker早在1961年就拒絕了馮諾依曼的關鍵假設,但直到1967年才發表對其的批評。[ 40 ])
愛因斯坦堅持認為量子力學不可能是一個完整的理論。他首選的論點依賴局部性原則:
- 考慮一個由兩個部分系統A和B組成的機械系統,這兩個部分系統僅在有限的時間內相互作用。給出它們相互作用之前的 ψ 函數。然後薛定諤方程式將在它們相互作用發生後提供 ψ 函數。現在讓我們盡可能透過測量完整地確定部分系統A的物理狀況。然後,量子力學允許我們根據所做的測量來確定部分系統B的 ψ 函數,以及整個系統的 ψ 函數。然而,該確定給出的結果取決於已測量到的指定A的條件的確定量值(例如坐標或動量)。 Since there can be only one physical condition of B after the interaction and which can reasonably not be considered as dependent on the particular measurement we perform on the system Aseparated from B it may be concluded that the ψ function is not unambiguously coordinated with the physical狀態.幾個 ψ 函數與系統B的相同物理條件的這種協調再次表明 ψ 函數不能被解釋為對單位系統物理條件的(完整)描述。[ 41 ]
EPR 思想實驗類似,也考慮由聯合波函數描述的兩個獨立系統A和B。然而,EPR 論文添加了後來被稱為 EPR 現實標準的想法,根據該標準,以概率 1 預測B測量結果的能力意味著B中存在“現實元素” 。[ 42 ]
1951 年,David Bohm提出了 EPR 思想實驗的變體,其中測量具有可能結果的離散範圍,這與 EPR 考慮的位置和動量測量不同。[ 43 ]前一年,吳健雄和歐文·沙克諾夫成功測量了糾纏對中產生的光子的偏振,從而使玻姆版本的 EPR 思想實驗變得切實可行。[ 44 ]
到 20 世紀 40 年代末,數學家喬治·麥基 (George Mackey)對量子物理學的基礎越來越感興趣,並於 1957 年制定了一系列假設,他認為這些假設是量子力學的精確定義。[ 45 ]麥基推測其中一個假設是多餘的,此後不久,安德魯·M·格里森證明它確實可以從其他假設中推導出來。[ 46 ] [ 47 ] 格里森定理提供了一個論點,即一大類隱變數理論與量子力學不相容。[註4 ]更具體地說,格里森定理排除了「非上下文」的隱藏變數模型。為了避免格里森定理的影響,任何量子力學的隱變量模型都必須涉及隱變量,這些隱變量不僅屬於被測系統的屬性,而且還依賴進行測量的外部環境。這種類型的依賴通常被認為是人為的或不受歡迎的。在某些情況下,它與狹義相對論不一致。[ 49 ] [ 50 ] Kochen-Specker 定理透過建構一個特定的有限射線子集來完善此陳述,在該子集上無法定義此類機率度量。[ 49 ] [ 51 ]
李政道在1960 年接近推導出貝爾定理。然而,由於 kaons 衰變,出現了複雜的情況,他並沒有推導出貝爾型不等式。[ 36 ]:308
貝爾的出版物
貝爾選擇在一本相對不起眼的期刊上發表他的定理,因為它不需要版面費,實際上是向當時在那裡發表論文的作者付費。然而,由於該期刊不提供免費的文章重印供作者分發,貝爾不得不用收到的錢購買副本,以便發送給其他物理學家。[ 52 ]雖然雜誌上刊登的文章本身將出版物的名稱簡單地列為“Physics”,但封面上卻帶有三語版本“Physics Physique Физика”,以反映它將印刷英語、法語和俄語的文章。[ 39 ]:92–100, 289
在證明 1964 年的結果之前,貝爾也證明了與 Kochen-Specker 定理等效的結果(因此後者有時也稱為 Bell-Kochen-Specker 或 Bell-KS 定理)。然而,這個定理的發表被無意地推遲到了 1966年。解決:愛因斯坦最不喜歡。[ 53 ]
實驗

源 S 產生成對的“光子”,並以相反的方向發送。每個光子都會遇到一個雙通道偏振器,其方向(a 或 b)可由實驗者設定。重合監視器偵測來自每個通道的新訊號並計數四種類型(++、−−、++− 和−+)的重合。
1967年,《Physics Physique Физика》這個不尋常的標題引起了約翰·克勞瑟的注意,他隨後發現了貝爾的論文,並開始考慮如何在實驗室進行貝爾測試。 [ 54 ] Clauser 和Stuart Freedman在1972年繼續進行了貝爾測試。 1982 年,Alain Aspect和合作者進行了第一次貝爾測試以消除這一限制。[ 57 ]這開始了逐漸嚴格的貝爾測試的趨勢。 GHZ 思想實驗於 2000 年使用糾纏的光子三重態在實踐中實施。[ 59 ]
在貝爾測試中,可能存在實驗設計或設定的問題,影響實驗結果的有效性。這些問題通常被稱為「漏洞」。實驗的目的是測試自然是否可以用局部隱變量理論來描述,這與量子力學的預測相矛盾。
實際實驗中最常見的漏洞是偵測和局部性漏洞。[ 60 ]當在實驗中檢測到一小部分粒子(通常是光子)時,檢測漏洞就被打開,使得可以通過假設檢測到的粒子是不具有代表性的樣本來解釋具有局部隱藏變量的數據。當檢測不是透過類空間分離完成時,局域性漏洞就會出現,使得一個測量的結果有可能影響另一個測量的結果,而不與相對論相矛盾。在某些實驗中,可能存在其他缺陷,使得貝爾測試違規的局部隱變量解釋成為可能。[ 61 ]
儘管局部性漏洞和檢測漏洞都已在不同的實驗中被封閉,但長期存在的挑戰是在同一個實驗中同時封閉這兩個漏洞。這最終在2015年的三個實驗中得以實現。 漏洞的”,但他表示,這些實驗“消除了我們應該放棄局部隱變量的最後疑慮”,並指出剩餘漏洞的例子是“牽強的”和“與物理學通常的推理方式不同”。[ 67 ]
這些透過實驗驗證貝爾不等式的違反情況的努力後來使克勞瑟、阿斯佩克特和安東·蔡林格榮獲 2022 年諾貝爾物理學獎。[ 68 ]
解釋
對貝爾定理的反應多種多樣。 Maximilian Schlosshauer、Johannes Kofler 和 Zeilinger 寫道,貝爾不等式提供了“一個很好的例子,說明我們如何透過大量實驗檢驗嚴格的理論結果,同時對其含義存在分歧。” [ 69 ]
哥本哈根詮釋
哥本哈根型解釋通常以違反貝爾不等式為理由拒絕通常被稱為反事實確定性或「實在論」的假設,這並不一定等同於放棄更廣泛的哲學意義上的實在論。[ 70 ] [ 71 ]例如,Roland Omnès主張拒絕隱變量,並得出結論:「量子力學可能與任何其範圍和成熟度的理論一樣現實」。[ 72 ] : 531 同樣,魯道夫·佩爾斯(Rudolf Peierls)認為貝爾定理的資訊是,由於局域性的前提是物理合理的,「在不放棄量子力學的一些結果的情況下不能引入隱變數」。[ 73 ] [ 74 ]
這也是源自哥本哈根傳統的解釋所走的路線,例如一致的歷史(通常被宣傳為「哥本哈根做得對」),[ 75 ]: 2839 以及QBism。[ 76 ]
量子力學的多世界解釋
多世界解釋,也稱為埃弗雷特解釋,是動態局部的,這意味著它不需要遠距離作用,[ 77 ]:17 並且是確定性的,因為它由量子力學的統一部分組成,沒有崩潰。它可以產生違反貝爾不等式的相關性,因為它違反了貝爾的隱含假設,即測量結果只有一個。事實上,貝爾定理可以在多世界框架中假設測量具有單一結果來證明。因此,違反貝爾不等式可以被解釋為測量有多種結果的證明。[ 78 ]
它對貝爾相關性的解釋是,當愛麗絲和鮑勃進行測量時,他們分裂成本地分支。從Alice的每個副本來看,Bob的多個副本都經歷著不同的結果,所以Bob不能有確定的結果,從Bob的每個副本來看也是如此。只有當它們未來的光錐重疊時,它們才會得到相互明確的結果。此時我們可以說貝爾相關性開始存在,但它是由純粹的局部機制產生的。因此,違反貝爾不等式不能被解釋為非定域性的證明。[ 77 ]: 28
非局部隱藏變數
大多數隱變量思想的擁護者認為實驗已經排除了局部隱變量。[註5 ]他們準備放棄局部性,透過非局部隱變數理論來解釋貝爾不等式的違反,其中粒子交換有關其狀態的資訊。這是量子力學的玻姆解釋的基礎,它要求宇宙中的所有粒子都能夠瞬時與所有其他粒子交換資訊。非局部隱變數理論面臨的一個挑戰是解釋為什麼這種瞬時通訊可以存在於隱變數層面,但不能用來發送訊號。[ 81 ] 2007 年的一項實驗排除了一大類非波姆非局部隱變量理論,儘管不是波姆力學本身。[ 82 ]
交易解釋假設波在時間上向後和向前傳播,同樣是非局域的。[ 83 ]
超決定論
推導貝爾定理的一個必要假設是隱藏變數與測量設定不相關。這個假設是合理的,因為實驗者有「自由意志」來選擇設置,並且首先有必要進行科學研究。測量的選擇必然與被測量的系統相關的(假設)理論被稱為超確定論。[ 60 ]
確定性模型的一些擁護者並沒有放棄局部隱變數。例如,傑拉德·特·霍夫特(Gerard 't Hooft)認為,不能忽視超決定論。[ 84 ]












































































沒有留言:
張貼留言
Love the Lord your God with all your heart and with all your soul and with all your mind.
耶 穌 對 他 說 : 你 要 盡 心 、 盡 性 、 盡 意 愛 主 ─ 你 的 神 。
—— Matthew 22:37 —— 馬 太 福 音 22:37